Question

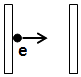
【题目】如图所示，虚线表示等势面，相邻等势面间的电势差相等，有一带电的小球在该电场中运动，不计小球的重力和空气阻力，实线表示该带正电小球的运动轨迹，小球在a点的动能等于20eV，运动到b点的动能等于2eV．若取c点为零电势点，则这个带电小球的电势能等于﹣6eV时，它的动能等于（ ）

A.16 eV
B.4 eV
C.6 eV
D.14 eV

Answer 1

【答案】D
【解析】解：设相邻两等势面间的电势差为U，小球的电荷量为q，小球从a到b和从b到c分别根据动能定理得：

﹣q3U=Ekb﹣Eka，qU=Ekc﹣Ekb

解得： eV=8eV

因为c点为零电势，所以小球在c点时的电势能为：Ec=qφc=0．

小球在电场中运动时，只有电场力做功，因此有W电=△Ek，同时，W电=﹣△Ep，所以△Ek+△Ep=0，即只有电场力做功时，小球的动能与电势能的总和保持不变．

设小球电势能为﹣6 eV时，在电场中的P点位置，由于小球的动能与电势能的总和保持8 eV不变，所以有EkP+Ep=8 eV，

解得：EkP=8 eV﹣Ep=[8﹣（﹣6）]eV=14 eV．

故答案为：D

能量守恒定律在电场中的应用，小球的电势能和动能之和保持不变。