Question

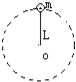
【题目】如图，一竖直放置的大圆环，在其水平直径上的A、B两端系着一根不可伸长的柔软细绳，绳上套有一光滑小铁环。现将大圆环在竖直平面内绕圆心O点逆时针缓缓转过一个微小角度，轻绳对A、B两点拉力，则（ ）

A. 变小 B. 变大

C. 轻绳对小铁环的作用力变大 D. 小铁环与O点总是在同一竖直线上

Answer 1

【答案】AD

【解析】设绳子是长度是2L，AB的长度是2l，AB水平时绳子与水平方向的夹角是α，平衡时两根绳子的拉力相等，设绳子拉力为F1，有：2F1sinα-mg=0，
得：FA=FB=F1＝
由图可知，cosα＝ ．
将大圆环绕着杆中点O在竖直平面内逆时针缓慢转过一个角度时，绳子与水平方向的夹角是θ，平衡时两根绳子的拉力仍然相等，设绳子拉力为F2，有：2F2sinθ-mg=0，
联立解得：FA′＝FB′＝．
设此时环到B的距离是L1，到A的距离是L2，则：L1+L2=2L
而由图可知，很显然：L1cosθ+L2cosθ＜2l，
即：cosθ＜得：α＜θ，所以：FA′=FB′＜FA=FB．即FA变小，FB变小，故A正确，B错误．
轻绳对小铁环的作用力等于小圆环的重力，则大小不变，选项C错误；当大圆环在竖直平面内绕圆心O点转动时，由几何知识可知，AB两点到圆心O的水平距离总相等，两侧绳子与竖直方向的夹角相等，则小铁环与O点总是在O点正下方的同一竖直线上，选项D正确；故选AD.