题目内容
2. 假设宇航员在某星球表面用长为L的轻绳栓一质量为m的小球,使之在竖直面内做圆周运动,如图所示,不计小球在最低点时与星球表面间的距离.小球恰好能运动至最高点,且在最高点时脱离轻绳,此后经时间t落至星球表面.已知万有引力常量为G,该星球半径为R,不考虑星球自转的影响.求:
假设宇航员在某星球表面用长为L的轻绳栓一质量为m的小球,使之在竖直面内做圆周运动,如图所示,不计小球在最低点时与星球表面间的距离.小球恰好能运动至最高点,且在最高点时脱离轻绳,此后经时间t落至星球表面.已知万有引力常量为G,该星球半径为R,不考虑星球自转的影响.求:(1)该星球表面的重力加速度g0和星球质量M;
(2)小球在最高点时速度v0的大小;
(3)若宇航员用此装置使小球在竖直面内又做了一次圆周运动,小球在最低点时的速度与(2)中的v0大小相等,则在最低点轻绳的拉力FT多大?
分析 (1)小球在最高点脱离绳子后做平抛运动,根据竖直方向做自由落体运动求出重力加速度,再根据星球表面,万有引力等于重力求解星球质量;
(2)小球恰好到达最高点,则在最高点由重力提供向心力,根据向心力公式求解;
(3)在最低点,根据向心力公式列式即可求解.
解答 解:(1)小球在最高点脱离绳子后做平抛运动,则有:
$2L=\frac{1}{2}{g}_{0}{t}^{2}$
解得:g0=$\frac{4L}{{t}^{2}}$,
在星球表面,万有引力等于重力,则有:
$G\frac{Mm}{{R}^{2}}=m{g}_{0}$
解得:M=$\frac{4L{R}^{2}}{G{t}^{2}}$
(2)小球恰好到达最高点,则在最高点由重力提供向心力,则有:
$m\frac{{{v}_{0}}^{2}}{L}=m{g}_{0}$
解得:${v}_{0}=\frac{2L}{t}$
(3)在最低点,根据向心力公式得:
FT-m${g}_{0}=m\frac{{{v}_{0}}^{2}}{L}$
解得:FT=$\frac{8mL}{{t}^{2}}$
答:(1)该星球表面的重力加速度g0为$\frac{4L}{{t}^{2}}$,星球质量M为$\frac{4L{R}^{2}}{G{t}^{2}}$;
(2)小球在最高点时速度v0的大小为$\frac{2L}{t}$;
(3)若宇航员用此装置使小球在竖直面内又做了一次圆周运动,小球在最低点时的速度与(2)中的v0大小相等,则在最低点轻绳的拉力FT为$\frac{8mL}{{t}^{2}}$.
点评 本题综合考查了平抛运动基本公式、牛顿第二定律、万有引力等于重力这些知识点,突破口是根据平抛运动求解重力加速度,知道小球恰好到达最高点,则在最高点由重力提供向心力,综合性较强,难度适中,需加强训练.

 阅读快车系列答案
阅读快车系列答案
| A. | 励磁线圈中的电流方向是逆时针方向 | |
| B. | 若只增大加速电压,可以使电子流的圆形径迹的半径增大 | |
| C. | 若只增大线圈中的电流,可以使电子流的圆形径迹的半径增大 | |
| D. | 若两线圈间的磁感应强度已知,灯丝发出的电子的初速为零,加速电压为U,则可通过测量圆形径迹的直径来估算电子的比荷 |
 如图所示是一半径为R的玻璃球体,0为球心,AB为水平直径,M点是玻璃球的最高点,来自B点的光线BD从D点射出,出射光线平行于AB,已知∠ABD=30°,光在真空中的传播速度为c,则( )
如图所示是一半径为R的玻璃球体,0为球心,AB为水平直径,M点是玻璃球的最高点,来自B点的光线BD从D点射出,出射光线平行于AB,已知∠ABD=30°,光在真空中的传播速度为c,则( )| A. | 此玻璃的折射率为$\frac{2}{3}$$\sqrt{3}$ | |
| B. | 光线从B传到D的时间为$\frac{3R}{c}$ | |
| C. | 若增大∠ABD,光线不可能在DM段发生全反射现象 | |
| D. | 若减小∠ABD,从AD段射出的光线均平行于AB |
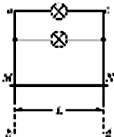 如图,两根足够长的金属导轨ab、cd竖直放置,导轨间距离为L,电阻不计.在导轨上端并接两个额定功率均为P、电阻均为R的小灯泡.整个系统置于匀强磁场中,磁感应强度方向与导轨所在平面垂直.现将一质量为m、电阻可以忽略的金属棒MN从图示位置由静止开始释放.金属棒下落过程中保持水平,且与导轨接触良好.已知某时刻后两灯泡保持正常发光.重力加速度为g.则( )
如图,两根足够长的金属导轨ab、cd竖直放置,导轨间距离为L,电阻不计.在导轨上端并接两个额定功率均为P、电阻均为R的小灯泡.整个系统置于匀强磁场中,磁感应强度方向与导轨所在平面垂直.现将一质量为m、电阻可以忽略的金属棒MN从图示位置由静止开始释放.金属棒下落过程中保持水平,且与导轨接触良好.已知某时刻后两灯泡保持正常发光.重力加速度为g.则( )| A. | 磁感应强度的大小为$\frac{mg}{2L}$$\sqrt{\frac{R}{P}}$ | |
| B. | 磁感应强度的大小为$\frac{mg}{2L}$$\sqrt{\frac{P}{R}}$ | |
| C. | 灯泡正常发光时导体棒的运动速率$\frac{mg}{2P}$ | |
| D. | 灯泡正常发光时导体棒的运动速率$\frac{2P}{mg}$ |
| A. | 关于原子核内部信息,最早来自天然放射性现象 | |
| B. | 结合能越大的原子核越稳定 | |
| C. | 目前核电站中主要利用的是轻核聚变产生的核能来发电 | |
| D. | 在核反应堆中常用的“慢化剂”有石墨、重水和普通水 | |
| E. | 在铀核的裂变中,当铀块的体积小于“临界体积”时,不能发生链式反应 |
 放在粗糙水平面上的物体受到水平拉力的作用,在0~6s内其速度与时间图象和该拉力的功率与时间图象分别如图所示,g=10m/s2,下列说法正确的是( )
放在粗糙水平面上的物体受到水平拉力的作用,在0~6s内其速度与时间图象和该拉力的功率与时间图象分别如图所示,g=10m/s2,下列说法正确的是( )| A. | 0~2 s内物体位移大小为12m | |
| B. | 0~2 s内拉力恒为5N | |
| C. | 合力在0~6 s内做的功与0~2 s内做的功均为30J | |
| D. | 动摩擦因素为μ=0.15 |
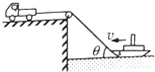 如图,汽车在平直路面上匀速运动,用跨过光滑定滑轮的轻绳牵引轮船,汽车与滑轮间的绳保持水平,当牵引轮船的绳与水平方向成θ角时,轮船速度为v,绳的拉力对船做功的功率为P,此时绳对船的拉力为$\frac{P}{vcosθ}$.若汽车还受到恒定阻力f,则汽车发动机的输出功率为fvcosθ+P.
如图,汽车在平直路面上匀速运动,用跨过光滑定滑轮的轻绳牵引轮船,汽车与滑轮间的绳保持水平,当牵引轮船的绳与水平方向成θ角时,轮船速度为v,绳的拉力对船做功的功率为P,此时绳对船的拉力为$\frac{P}{vcosθ}$.若汽车还受到恒定阻力f,则汽车发动机的输出功率为fvcosθ+P.