题目内容
20.某同学用如图甲所示的装置通过研究重锤的落体运动来验证机械能守恒定律.已知重力加速度为g.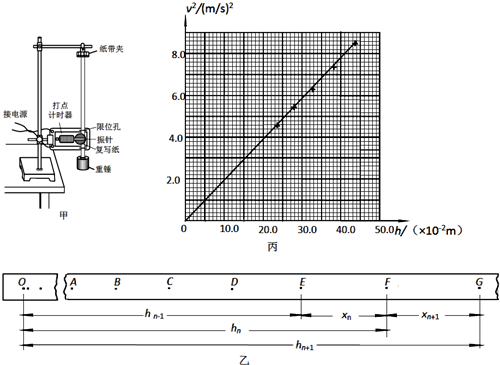
①在实验所需的物理量中,需要直接测量的是B,通过计算得到的是D.(填写代号)
A.重锤的质量
B.重锤下落的高度
C.重锤底部距水平地面的高度
D.与下落高度对应的重锤的瞬时速度
②在实验得到的纸带中,我们选用如图乙所示的起点O与相邻点之间距离约为2mm的纸带来验证机械能守恒定律.图中A、B、C、D、E、F、G为七个相邻的原始点,F点是第n个点.设相邻点间的时间间隔为T,下列表达式可以用在本实验中计算F点速度vF的是C.
A.vF=g(nT ) B.vF=$\sqrt{2g{h}_{n}}$ C.vF=$\frac{{h}_{n+1}-{h}_{n-1}}{2T}$ D.vF=$\frac{{x}_{n+1}-{x}_{n}}{2T}$
③若代入图乙中所测的数据,求得$\frac{1}{2}{v}_{n}^{2}$在差范围内等于ghn(用已知量和图乙中测出的物理量表示),即可验证重锤下落过程中机械能守恒.即使在操作及测量无误的前提下,所求$\frac{1}{2}{v}_{n}^{2}$也一定会略小于(选填“大于”或“小于”)后者的计算值,这是实验存在系统误差的必然结果.
④另一名同学利用图乙所示的纸带,分别测量出各点到起始点的距离h,并分别计算出各点的速度v,绘出v2-h图线,如图丙所示.从v2-h图线求得重锤下落的加速度g′=9.80m/s2( 保留3位有效数字 ).则由上述方法可知,这名同学是通过观察v2-h图线是否过原点,以及判断g与g′(用相关物理量的字母符号表示)在实验误差允许的范围内是否相等,来验证机械能是否守恒的.
分析 验证机械能守恒定律的实验原理是:以自由落体运动为例,需要验证的方程是:mgh=$\frac{1}{2}$mv2,根据实验原理得到要验证的表达式,确定待测量.
该实验是验证机械能守恒定律的实验,不能把重物看成自由落体运动,再运用自由落体的规律求解速度,那么就不需要验证了,求速度时我们是利用匀变速直线运动的规律即匀变速直线运动中时间中点的瞬时速度等于该过程中的平均速度;
根据机械能守恒得出v2-h的关系式,结合图线的斜率求出重锤下落的加速度.
解答 解:①重锤的质量可测可不测,因为动能的增加量和重力势能的减小量式子中都有质量,可以约去.需要测量的物理量是B:重锤下落的高度,
通过计算得到的物理量是D:与下落高度对应的重锤的瞬时速度.
②A、该实验是验证机械能守恒定律的实验,不能把重物看成自由落体运动,再运用自由落体的规律求解速度,那么就不需要验证了,A、B都是利用了自由落体运动规律求速度的,故AB错误;
C、求速度时我们是利用匀变速直线运动的规律即匀变速直线运动中时间中点的瞬时速度等于该过程中的平均速度,
vF=$\frac{EG}{2T}$=$\frac{{h}_{n+1}-{h}_{n-1}}{2T}$=$\frac{{x}_{n}+{x}_{n+1}}{2T}$,故C正确,D错误.
故选:C.
(3)需要验证的方程是:mgh=$\frac{1}{2}$mv2,
若代入图乙中所测的数据,求得$\frac{1}{2}$vn2在误差范围内等于ghn,即可验证重锤下落过程中机械能守恒.即使在操作及测量无误的前提下,
由于存在空气阻力或者限位孔和纸带之间存在摩擦,所求$\frac{1}{2}$vn2也一定会略小于后者的计算值,这是实验存在系统误差的必然结果.
(4)根据mgh=$\frac{1}{2}$mv2得:v2=2gh,
可知图线的斜率等于2g′,
则:g′=$\frac{k}{2}$.
图线的斜率为:k=$\frac{8.0-3.0}{0.415-0.16}$=19.60.,
则:g′=9.80m/s2.
则由上述方法可知,这名同学是通过观察v2-h图线是否过原点,以及判断g与 g′在实验误差允许的范围内是否相等,来验证机械能是否守恒的.
故答案为:①B; D
②C
③ghn; 小于
④9.80; g; g′
点评 本题考查验证机械能守恒定律的实验,在解决实验问题时要注意实验的原理有实验中的注意事项,特别要注意数据的处理及图象的应用.
对于基础实验要从实验原理出发去理解,要亲自动手实验,深刻体会实验的具体操作,不能单凭记忆去理解实验.

 智能训练练测考系列答案
智能训练练测考系列答案| A. | 随着温度的升高,一方面各种波长的辐射强度都会增加;另一方面辐射强度的极大值向波长较短的方向移动 | |
| B. | 在康普顿效应中,当入射光子与晶体中的电子碰撞时,把一部分动量转移给电子,因此,光子散射后波长变短 | |
| C. | 根据海森伯提出的不确定性关系可知,不可能同时准确地测定微观粒子的位置和动量 | |
| D. | 物质波和光波都是概率波 |
 图示的保温瓶里用软木塞密封了半瓶开水,经一夜后软木塞很难取出.与刚把软木塞盖上相比,在单位时间内,保温瓶内壁单位面积上被气体分子撞击的次数减小(选填“增大”、“不变”或“减小”),瓶内气体的相对湿度增大(选填“增大”、“不变”或“减小”).
图示的保温瓶里用软木塞密封了半瓶开水,经一夜后软木塞很难取出.与刚把软木塞盖上相比,在单位时间内,保温瓶内壁单位面积上被气体分子撞击的次数减小(选填“增大”、“不变”或“减小”),瓶内气体的相对湿度增大(选填“增大”、“不变”或“减小”). 在“探究功与速度变化的关系”实验中.
在“探究功与速度变化的关系”实验中. 在描绘小电珠的伏安特性曲线实验中:
在描绘小电珠的伏安特性曲线实验中:
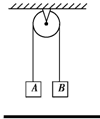 如图所示,两个质量各为m1和m2的小物块A和B,分别系在一条跨过光滑定滑轮的软绳两端,已知m1>m2,现要利用此装置验证机械能守恒定律.方法如下:
如图所示,两个质量各为m1和m2的小物块A和B,分别系在一条跨过光滑定滑轮的软绳两端,已知m1>m2,现要利用此装置验证机械能守恒定律.方法如下: 城市晚上或者每逢节日,同学们往往能看到许多霓虹灯发出鲜艳绚丽的灯光,将城市装扮得异彩纷呈,赏心悦目.频率为50Hz的交变电流,其电压u=168sinωt V,把它加在激发电压、熄灭电压均为84V的霓虹灯的两端,求在半个周期内霓虹灯点亮的时间.
城市晚上或者每逢节日,同学们往往能看到许多霓虹灯发出鲜艳绚丽的灯光,将城市装扮得异彩纷呈,赏心悦目.频率为50Hz的交变电流,其电压u=168sinωt V,把它加在激发电压、熄灭电压均为84V的霓虹灯的两端,求在半个周期内霓虹灯点亮的时间.