题目内容
4.两根相距L=0.5m的足够长的金属导轨如图甲所示放置,他们各有一边在同一水平面上,另一边垂直于水平面.金属细杆ab、cd的质量均为m=0.05kg,电阻均为R=1.0Ω,它们与导轨垂直接触形成闭合回路,杆与导轨之间的动摩擦因数μ=0.5,导轨电阻不计.整个装置处于磁感应强度大小B=1.0T、方向竖直向上的匀强磁场中.当ab杆在平行于水平导轨的拉力F作用下沿导轨向右运动时,从某一时刻开始释放cd杆,并且开始计时,cd杆运动速度c随时间变化的图象如图乙所示(在0~1.0s和2.0~3.0s内,cd做匀变速直线运动.g=10m/s2 ).求:(1)在0~1.0s时间内,回路中感应电流I1的大小;
(2)在0~3.0s时间内,ab杆在水平导轨上运动的最大速度Vm;
(3)已知1.0~2.0s内,ab杆做匀加速直线运动,写出1.0~2.0s内拉力F随时间t变化的关系式,并在图丙中画出在0~3.0s内,拉力F随时间t变化的图象.(不需要写出计算过程,只需写出表达式和画出图线)

分析 (1)由图看出,在0~1.0s时间内,cd杆做匀加速直线运动,所受的安培力是恒力,根据速度图象的斜率求出加速度,由牛顿第二定律和安培力公式求解回路中感应电流的大小;
(2)在2s~3s时间内,cd杆做匀减速直线运动,安培力最大.由图象的斜率求出加速度,根据牛顿第二定律可求出回路中感应电流的大小;由闭合电路欧姆定律
(3)分段由牛顿第二定律求出拉力,再作出图象.
解答 解:(1)在0~1s时间内,cd杆向下做匀加速运动,
由乙图可知:${a_1}=\frac{{{V_1}-{V_0}}}{t}=4m/{s^2}$,
对cd杆进行受力分析,根据牛顿第二定律有:
在竖直方向上:mg-f1=ma1,
在水平方向上:N1-F安1=0 F安1=I1LB f1=μN1=μBI1L,
解得:${I_1}=\frac{{m(g-{a_1})}}{μBL}=\frac{0.05×(10-4)}{0.5×1×0.5}=1.2A$;
(2)在2~3s时间内,cd杆向下做匀减速运动时,
由乙图可知,加速度:${a_3}=\frac{{{V_2}-{V_3}}}{t}=4m/{s^2}$,
对cd杆进行受力分析,根据牛顿第二定律有:
在竖直方向上:f3-mg=ma3 ,
在水平方向上:N3-F安3=0 F安3=I3LB f3=μN3=μBI3L,
解得:${I_3}=\frac{{m(g+{a_3})}}{μBL}=\frac{0.05×(10+4)}{0.5×1×0.5}=2.8A$,
电动势:E3=I3×2R=5.6V,感应电动势:E3=BLV3,
ab杆的最大速度为:${V_m}={V_3}=\frac{E_3}{BL}=11.2m/s$; 
(3)在0~1.0s内,ab杆做匀速运动:F1=BI1L+μmg=0.85N,${V_1}=\frac{{2{I_1}R}}{BL}=4.8m/s$,
在2.0~3.0s内,ab杆做匀速运动:F3=BI3L+μmg=1.65N,${V_3}=\frac{{2{I_3}R}}{BL}=11.2m/s$,
在1~2s内,ab杆做匀加速运动,加速度为:${a_2}=\frac{{{V_3}-{V_1}}}{t_2}=6.4m/{s^2}$,
对ab杆分析,根据牛顿第二定律有:$F-μmg-\frac{{{B^2}{L^2}[{V_1}+{a_2}(t-1)]}}{2R}=m{a_2}$(1s<t<2s)
所以表达式为:F=1.17+0.8(t-1)(1s<t<2s)
当t=1s时拉力为:F2min=1.17N
当t=2s时拉力为:F2max=1.97N
在0~3.0s内,拉力F随时间t变化的图象如图所示:
答:(1)在0~1.0s时间内,回路中感应电流I1的大小1.2A;
(2)在0~3.0s时间内,ab杆在水平导轨上运动的最大速度Vm为11.2m/s;
(3)已知1.0~2.0s内,ab杆做匀加速直线运动,1.0~2.0s内拉力F随时间t变化的关系式为:F=1.17+0.8(t-1)(1s<t<2s),在0~3.0s内,拉力F随时间t变化的图象如图所示.
点评 本题涉及电磁感应过程中的复杂受力分析,解决这类问题的关键是,根据法拉第电磁感应定律求解感应电动势,然后根据牛顿第二定律求解拉力的大小,进一步根据运动状态列方程求解.

 一物体自t=0时由静止开始向上做直线运动,其a-t图象如图所示,则下列判断正确的是( )
一物体自t=0时由静止开始向上做直线运动,其a-t图象如图所示,则下列判断正确的是( )| A. | 在第4s时,物体离出发点最远 | |
| B. | 在0-6s内,物体的平均速度为3m/s | |
| C. | 在2-4s内,物体的机械能守恒 | |
| D. | 在4-6s内,物体所受的合外力做负功 |
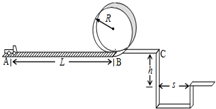 某校物理兴趣小组决定举行遥控赛车比赛.比赛路径如图所示,赛车静止起从起点A出发,沿粗糙水平直线轨道运动L后,由B点进入半径为R的光滑竖直圆轨道,离开竖直圆轨道后继续在光滑平直轨道上运动到C点,并能跃过壕沟.已知赛车质量为m=0.1kg,通电后以额定功率P=1.8W工作,在粗糙水平轨道运动时受到的摩擦阻力恒为Ff=0.25N.图中L=12m、R=0.32m,h=1.25m,s=1.50m,g=10m/s2.求:要使赛车能完成比赛,电动机工作的最短时间t.
某校物理兴趣小组决定举行遥控赛车比赛.比赛路径如图所示,赛车静止起从起点A出发,沿粗糙水平直线轨道运动L后,由B点进入半径为R的光滑竖直圆轨道,离开竖直圆轨道后继续在光滑平直轨道上运动到C点,并能跃过壕沟.已知赛车质量为m=0.1kg,通电后以额定功率P=1.8W工作,在粗糙水平轨道运动时受到的摩擦阻力恒为Ff=0.25N.图中L=12m、R=0.32m,h=1.25m,s=1.50m,g=10m/s2.求:要使赛车能完成比赛,电动机工作的最短时间t.
 如图所示,半径为r的金属环绕通过其直径的轴OO′,以角速度ω做匀速转动,金属环的电阻值为R,匀强磁场的磁感应强度为B,从金属环的平面与磁场方向重合时开始计时,
如图所示,半径为r的金属环绕通过其直径的轴OO′,以角速度ω做匀速转动,金属环的电阻值为R,匀强磁场的磁感应强度为B,从金属环的平面与磁场方向重合时开始计时, 如图所示,一滑块经水平轨道AB,进入竖直平面内的四分之一圆弧轨道BC.已知滑动的质量m=0.6kg,在A点的速度vA=8.0m/s,AB长x=5.0m,滑动与水平轨道间的动摩擦因数μ=0.15,圆弧轨道的半径R=2.0m,滑动离开C点后竖直上升h=0.2m,取g=10m/s2.求:
如图所示,一滑块经水平轨道AB,进入竖直平面内的四分之一圆弧轨道BC.已知滑动的质量m=0.6kg,在A点的速度vA=8.0m/s,AB长x=5.0m,滑动与水平轨道间的动摩擦因数μ=0.15,圆弧轨道的半径R=2.0m,滑动离开C点后竖直上升h=0.2m,取g=10m/s2.求: