Question

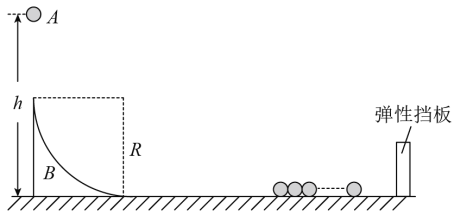
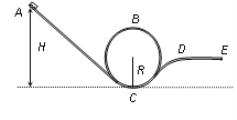
【题目】如图所示，是游乐场翻滚过山车示意图，斜面轨道AC、弯曲、水平轨道CDE和半径R的竖直圆形轨道平滑连接。质量m的小车，从距水平面H高处的A点静止释放，通过最低点C后沿圆形轨道运动一周后进入弯曲、水平轨道CDE。重力加速度g，不计摩擦力和阻力。求：

(1)若小车从A点静止释放到达圆形轨道最低点C时的速度大小；

(2)小车在圆形轨道最高点B时轨道对小车的作用力；

(3)为使小车通过圆形轨道的B点，相对于C点的水平面小车下落高度h需要满足的条件。

Answer 1

【答案】(1)；(2)；(3)大于等于2.5R

【解析】

(1)不计摩擦力和阻力，小车下滑过程中机械能守恒

解得

(2)设小车在圆形轨道最高点B的速度为vB，轨道对小车的作用力为N，有

由机械能守恒可得

解得

(3)设小车在圆形轨道最高点B恰好不脱离轨道时的速度为v，则根据牛顿第二定律及机械能守恒定律可得

，

解得

h=2.5R

为使小车能通过圆形轨道的最高点B，相对于C点的水平面小车下落高度要大于等于2.5R。