题目内容
【题目】如图所示为研究电子枪中电子在电场中运动的简化模型示意图.在xoy平面的第一象限,存在以![]() 轴、
轴、![]() 轴及双曲线
轴及双曲线![]() 的一段(0≤
的一段(0≤![]() ≤L,0≤
≤L,0≤![]() ≤L)为边界的匀强电场区域Ⅰ;在第二象限存在以
≤L)为边界的匀强电场区域Ⅰ;在第二象限存在以![]() =-L、
=-L、![]() =-2L、
=-2L、![]() =0、
=0、![]() =L的匀强电场区域Ⅱ.两个电场大小均为E,不计电子所受重力,电子的电荷量为e,则:
=L的匀强电场区域Ⅱ.两个电场大小均为E,不计电子所受重力,电子的电荷量为e,则:

(1)从电场Ⅰ的边界B点处静止释放电子,电子离开MNPQ时的位置坐标;
(2)从电场I的AB曲线边界处由静止释放电子,电子离开MNPQ时的最小动能;
(3)若将左侧电场II整体水平向左移动![]() (n≥1),要使电子从
(n≥1),要使电子从![]() =-2L,
=-2L,![]() =0处离开电场区域II,在电场I区域内由静止释放电子的所有位置。
=0处离开电场区域II,在电场I区域内由静止释放电子的所有位置。
【答案】(1)(-2L,0)(2)EeL(3)![]()
【解析】(1)证明:设在Ⅰ区域的AB曲线边界上任一点(x,y)释放电子,离开Ⅰ区域时的速度
![]()
以v1的速度匀速运动到匀强电场II的右边界,在电场II内做类平抛运动,设初速度方向上可以通过电场II区到其左边界,则时间t=![]()
在电场方向上发生的位移![]()
![]()
求得![]() 即正好通过P点
即正好通过P点
(2)设在Ⅰ区域的AB曲线边界上任一点(x,y)释放电子,离开Ⅰ区域时的速度
![]()
进入II区后偏转,离开II区时在电场方向上的速度![]()
t=![]()
![]() 得
得![]()
电子离开MNPQ时的动能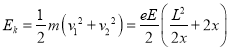
当![]() 时,即x=L/2时有EK最小值=eEL
时,即x=L/2时有EK最小值=eEL
(3)设在Ⅰ区域内的任一点(x,y)释放电子,离开Ⅰ区域时的速度
![]()
以v1的速度匀速运动到匀强电场II的右边界,在电场II内做类平抛运动,要其能通过
x=-2L,y=0处,有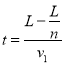
![]()
![]()
代入化简得![]() (0≤x≤L,0≤y≤L)
(0≤x≤L,0≤y≤L)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】(1)为完成“探究变压器线圈两端的电压与匝数的关系”的实验,必须要选用的是________(多选).
A.有闭合铁芯的原副线圈
B.无铁芯的原副线圈
C.交流电源
D.直流电源
E.多用电表(交流电压挡)
F.多用电表(交流电流挡)
用匝数na=60匝和nb=120匝的变压器,实验测量数据如下表:
U1/V | 1.80 | 2.80 | 3.80 | 4.90 |
U2/V | 4.00 | 6.01 | 8.02 | 9.98 |
根据测量数据可判断连接电源的线圈是___________(填“na”或“nb”).
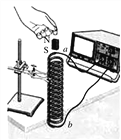
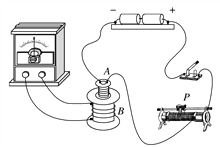
(2)用如图所示的装置做“探究感应电流方向的规律”实验,磁体从靠近线圈的上方静止下落,当磁体运动到如图所示的位置时,流过线圈的感应电流方向从 ________(填“a到b”或“b到a”).在磁体穿过整个线圈的过程中,传感器显示的电流i随时间t的图象应该是__________.