题目内容
【题目】如图甲所示,质量为m=1kg的物体置于倾角为θ=30°的固定且足够长的光滑斜面上,对物体施以平行于斜面向上的拉力F,t1=5s时撤去拉力,物体撤去拉力前运动的v﹣t图象如图乙所示.试求:(g取10m/s2)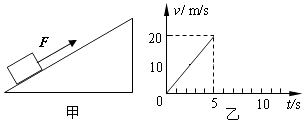
(1)拉力F的大小
(2)物体在11s内的位移.
【答案】
(1)解:由v﹣t图象知力F作用时a1= ![]() =
= ![]() =4m/s2,
=4m/s2,
根据牛顿第二定律:F﹣mgsin30°=ma1,
解得:F=mgsin30°+ma1=10× ![]() =9N
=9N
答:拉力F的大小为9N
(2)解:撤去拉力后物体减速上滑的加速度大小为a2,
根据牛顿第二定律可得:a2=gsinθ=5m/s2,
物体在5s末的速度为v1=a1t1=4×5m/s=20m/s,
此过程的位移大小为:x1= ![]() ,
,
物体上升到最高点的时间为:t2= ![]() ,
,
此过程的位移大小为:x2= ![]() ,
,
此后t3=11s﹣9s=2s时间内物体沿斜面下滑,下滑的位移为:
x3= ![]() ,
,
所以物体在11s内的位移为x=x1+x2﹣x3=50m+40m﹣10m=80m,方向沿斜面向上.
答:物体在11s内的位移大小为80m,方向沿斜面向上
【解析】(1)由v﹣t图象的斜率表示加速度先求出拉力作用时的加速度,然后以物体为研究对象,受力分析,根据牛顿第二定律列方程求解;(2)先求出撤去拉力后物体停止所用的时间,然后分析物体的运动过程,根据牛顿第二定律求解加速度、再根据位移时间关系分别求出各段位移,再求总位移.
【考点精析】解答此题的关键在于理解V-t图象的相关知识,掌握v-t图像:①在速度图像中,可以读出物体在任何时刻的速度;②在速度图像中,物体在一段时间内的位移大小等于物体的速度图像与这段时间轴所围面积的值;③在速度图像中,物体在任意时刻的加速度就是速度图像上所对应的点的切线的斜率;④图线与横轴交叉,表示物体运动的速度反向;⑤图线是直线表示物体做匀变速直线运动或匀速直线运动;图线是曲线表示物体做变加速运动.