题目内容

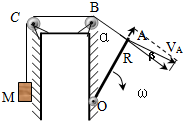
（1）如图1所示，杆OA长为R，可绕过O点的水平轴在竖直平面内转动，其端点A系着一跨过定滑轮B、C的不可伸长的轻绳，绳的另一端系一物块M．滑轮的半径可忽略，B在O的正上方，OB之间的距离为H．某一时刻，当绳的BA段与OB之间的夹角为α时，杆的角速度为ω，求此时物块M的速率Vm．
（2）一探照灯照射在云层底面上，这底面是与地面平行的平面．如图2所示，云层底面高h，探照灯以匀角速度ω在竖直平面内转动，当光束转过与竖直线夹角为θ时，此刻云层底面上光点的移动速度是多大？
分析：（1）根据v=ωr求解A的速度，然后将A点的速度沿着平行绳子方向和垂直绳子方向正交分解，重物速度等于平行绳子方向的分速度；
（2）云层底面上光点的移动速度沿着光线方向和垂直光线方向正交分解，其中垂直光线方向分速度与半径的比值等于杆的转动角速度．
解答：解：（1）杆的端点A点绕O点作圆周运动，其速度VA的方向与杆OA垂直，在所考察时其速度大小为：VA=ωR
对于速度VA作如图所示的正交分解，即沿绳BA方向和垂直于BA方向进行分解，沿绳BA方向的分量就是物块M的速率VM，因为物块只有沿绳方向的速度，所以：VM=VAcosβ

由正弦定理知，
sin(
π
2
+β)
H
=
sinα
R

由以上各式得VM=ωHsinα．
（2）当光束转过θ角时，光照射在云层上的位置到灯的距离为：L=
h
cosθ

这个位置光束的端点沿切线方向的线速度为：v=ωL=
hω
cosθ

云层底面上光点的移动速度为：v′=
v
cosθ
=
hω
cos2θ

答：（1）此时物块M的速率为ωHsinα．
（2）此刻云层底面上光点的移动速度是
hω
cos2θ
．
点评：本题第一问与第二问关键是运用运动的合成与分解的方法求解，找出合速度与分速度是关键．
练习册系列答案
相关题目
[物理--选修3-5]
（1）如图1所示，为氢原子的能级图．若在气体放电管中，处于基态的氢原子受到能量为12.8eV的高速电子轰击而跃迁到激发态，在这些氢原子从激发态向低能级跃迁的过程中
BD
BD

A．最多能辐射出10种不同频率的光子
B．最多能辐射出6种不同频率的光子
C．能辐射出的波长最长的光子是从n=5跃迁到n=4能级时放出的
D．能辐射出的波长最长的光子是从n=4跃迁到n=3能级时放出的
（2）如图2所示，质量M=2kg的滑块套在光滑的水平轨道上，质量m=1kg的小球（视为质点）通过长L=0.5m的轻杆与滑块上的光滑轴O连接，滑块不会影响到小球和轻杆在竖直平面内绕O轴的转动．开始时轻杆处于水平状态．现给小球一个大小为v0的竖直向下的初速度，取g=10m/s2．

（a）若锁定滑块，要使小球在绕O轴转动时恰能通过圆周的最高点，求初速度v0的大小．
（b）若解除对滑块的锁定，并让小球竖直向下的初速度v′0=3m/s，试求小球相对于初始位置能上升的最大高度．
选做题
（1）如图1所示为某种放射性元素的衰变规律（纵坐标
n
n0
表示任意时刻放射性元素的原子数与t=0时的原子数之比），则该放射性元素的半衰期是
 
天（一个月按30天计算）．在从某古迹中发掘出来的木材中，所含
 
14
6
C 的比例是正在生长的植物中的80%，放射性
 
14
6
C的半衰期是5700年，根据图象可以推算，该古迹距今约
 
年．
（2）如图2所示，在光滑水平地面上，质量为M的滑块上用轻杆及轻绳悬吊质量为m的小球，轻绳的长度为L．此装置一起以速度v0向右滑动．另一质量也为M的滑块静止于上述装置的右侧．当两滑块相撞后，便粘在一起向右运动，求：
①两滑块相撞过程中损失的机械能；
②当小球向右摆到最大高度时两滑块的速度大小．精英家教网
[物理--选修3-5]
（1）如图1所示，为氢原子的能级图．若在气体放电管中，处于基态的氢原子受到能量为12.8eV的高速电子轰击而跃迁到激发态，在这些氢原子从激发态向低能级跃迁的过程中______
A．最多能辐射出10种不同频率的光子
B．最多能辐射出6种不同频率的光子
C．能辐射出的波长最长的光子是从n=5跃迁到n=4能级时放出的
D．能辐射出的波长最长的光子是从n=4跃迁到n=3能级时放出的
（2）如图2所示，质量M=2kg的滑块套在光滑的水平轨道上，质量m=1kg的小球（视为质点）通过长L=0.5m的轻杆与滑块上的光滑轴O连接，滑块不会影响到小球和轻杆在竖直平面内绕O轴的转动．开始时轻杆处于水平状态．现给小球一个大小为v的竖直向下的初速度，取g=10m/s2．

（a）若锁定滑块，要使小球在绕O轴转动时恰能通过圆周的最高点，求初速度v的大小．
（b）若解除对滑块的锁定，并让小球竖直向下的初速度v′=3m/s，试求小球相对于初始位置能上升的最大高度．

第一部分  力＆物体的平衡

第一讲 力的处理

一、矢量的运算

1、加法

表达： +  =  。

名词：为“和矢量”。

法则：平行四边形法则。如图1所示。

和矢量大小：c =  ，其中α为和的夹角。

和矢量方向：在、之间，和夹角β= arcsin

2、减法

表达： = － 。

名词：为“被减数矢量”，为“减数矢量”，为“差矢量”。

法则：三角形法则。如图2所示。将被减数矢量和减数矢量的起始端平移到一点，然后连接两时量末端，指向被减数时量的时量，即是差矢量。

差矢量大小：a =  ，其中θ为和的夹角。

差矢量的方向可以用正弦定理求得。

一条直线上的矢量运算是平行四边形和三角形法则的特例。

例题：已知质点做匀速率圆周运动，半径为R ，周期为T ，求它在T内和在T内的平均加速度大小。

解说：如图3所示，A到B点对应T的过程，A到C点对应T的过程。这三点的速度矢量分别设为、和。

根据加速度的定义 = 得：= ，= 

由于有两处涉及矢量减法，设两个差矢量 = － ，= － ，根据三角形法则，它们在图3中的大小、方向已绘出（的“三角形”已被拉伸成一条直线）。

本题只关心各矢量的大小，显然：

 =  =  =  ，且： = =  ， = 2= 

所以：=  =  =  ，=  =  =  。

（学生活动）观察与思考：这两个加速度是否相等，匀速率圆周运动是不是匀变速运动？

答：否；不是。

3、乘法

矢量的乘法有两种：叉乘和点乘，和代数的乘法有着质的不同。

⑴ 叉乘

表达：× = 

名词：称“矢量的叉积”，它是一个新的矢量。

叉积的大小：c = absinα，其中α为和的夹角。意义：的大小对应由和作成的平行四边形的面积。

叉积的方向：垂直和确定的平面，并由右手螺旋定则确定方向，如图4所示。

显然，×≠×，但有：×= －×

⑵ 点乘

表达：· = c

名词：c称“矢量的点积”，它不再是一个矢量，而是一个标量。

点积的大小：c = abcosα，其中α为和的夹角。

二、共点力的合成

1、平行四边形法则与矢量表达式

2、一般平行四边形的合力与分力的求法

余弦定理（或分割成RtΔ）解合力的大小

正弦定理解方向

三、力的分解

1、按效果分解

2、按需要——正交分解

第二讲 物体的平衡

一、共点力平衡

1、特征：质心无加速度。

2、条件：Σ = 0 ，或  = 0 ， = 0

例题：如图5所示，长为L 、粗细不均匀的横杆被两根轻绳水平悬挂，绳子与水平方向的夹角在图上已标示，求横杆的重心位置。

解说：直接用三力共点的知识解题，几何关系比较简单。

答案：距棒的左端L/4处。

（学生活动）思考：放在斜面上的均质长方体，按实际情况分析受力，斜面的支持力会通过长方体的重心吗？

解：将各处的支持力归纳成一个N ，则长方体受三个力（G 、f 、N）必共点，由此推知，N不可能通过长方体的重心。正确受力情形如图6所示（通常的受力图是将受力物体看成一个点，这时，N就过重心了）。

答：不会。

二、转动平衡

1、特征：物体无转动加速度。

2、条件：Σ= 0 ，或ΣM+ =ΣM- 

如果物体静止，肯定会同时满足两种平衡，因此用两种思路均可解题。

3、非共点力的合成

大小和方向：遵从一条直线矢量合成法则。

作用点：先假定一个等效作用点，然后让所有的平行力对这个作用点的和力矩为零。

第三讲 习题课

1、如图7所示，在固定的、倾角为α斜面上，有一块可以转动的夹板（β不定），夹板和斜面夹着一个质量为m的光滑均质球体，试求：β取何值时，夹板对球的弹力最小。

解说：法一，平行四边形动态处理。

对球体进行受力分析，然后对平行四边形中的矢量G和N1进行平移，使它们构成一个三角形，如图8的左图和中图所示。

由于G的大小和方向均不变，而N1的方向不可变，当β增大导致N2的方向改变时，N2的变化和N1的方向变化如图8的右图所示。

显然，随着β增大，N1单调减小，而N2的大小先减小后增大，当N2垂直N1时，N2取极小值，且N2min = Gsinα。

法二，函数法。

看图8的中间图，对这个三角形用正弦定理，有：

 =  ，即：N2 =  ，β在0到180°之间取值，N2的极值讨论是很容易的。

答案：当β= 90°时，甲板的弹力最小。

2、把一个重为G的物体用一个水平推力F压在竖直的足够高的墙壁上，F随时间t的变化规律如图9所示，则在t = 0开始物体所受的摩擦力f的变化图线是图10中的哪一个？

解说：静力学旨在解决静态问题和准静态过程的问题，但本题是一个例外。物体在竖直方向的运动先加速后减速，平衡方程不再适用。如何避开牛顿第二定律，是本题授课时的难点。

静力学的知识，本题在于区分两种摩擦的不同判据。

水平方向合力为零，得：支持力N持续增大。

物体在运动时，滑动摩擦力f = μN ，必持续增大。但物体在静止后静摩擦力f′≡ G ，与N没有关系。

对运动过程加以分析，物体必有加速和减速两个过程。据物理常识，加速时，f ＜ G ，而在减速时f ＞ G 。

答案：B 。

3、如图11所示，一个重量为G的小球套在竖直放置的、半径为R的光滑大环上，另一轻质弹簧的劲度系数为k ，自由长度为L（L＜2R），一端固定在大圆环的顶点A ，另一端与小球相连。环静止平衡时位于大环上的B点。试求弹簧与竖直方向的夹角θ。

解说：平行四边形的三个矢量总是可以平移到一个三角形中去讨论，解三角形的典型思路有三种：①分割成直角三角形（或本来就是直角三角形）；②利用正、余弦定理；③利用力学矢量三角形和某空间位置三角形相似。本题旨在贯彻第三种思路。

分析小球受力→矢量平移，如图12所示，其中F表示弹簧弹力，N表示大环的支持力。

（学生活动）思考：支持力N可不可以沿图12中的反方向？（正交分解看水平方向平衡——不可以。）

容易判断，图中的灰色矢量三角形和空间位置三角形ΔAOB是相似的，所以：

                                   ⑴

由胡克定律：F = k（- R）                ⑵

几何关系：= 2Rcosθ                     ⑶

解以上三式即可。

答案：arccos 。

（学生活动）思考：若将弹簧换成劲度系数k′较大的弹簧，其它条件不变，则弹簧弹力怎么变？环的支持力怎么变？

答：变小；不变。

（学生活动）反馈练习：光滑半球固定在水平面上，球心O的正上方有一定滑轮，一根轻绳跨过滑轮将一小球从图13所示的A位置开始缓慢拉至B位置。试判断：在此过程中，绳子的拉力T和球面支持力N怎样变化？

解：和上题完全相同。

答：T变小，N不变。

4、如图14所示，一个半径为R的非均质圆球，其重心不在球心O点，先将它置于水平地面上，平衡时球面上的A点和地面接触；再将它置于倾角为30°的粗糙斜面上，平衡时球面上的B点与斜面接触，已知A到B的圆心角也为30°。试求球体的重心C到球心O的距离。

解说：练习三力共点的应用。

根据在平面上的平衡，可知重心C在OA连线上。根据在斜面上的平衡，支持力、重力和静摩擦力共点，可以画出重心的具体位置。几何计算比较简单。

答案：R 。

（学生活动）反馈练习：静摩擦足够，将长为a 、厚为b的砖块码在倾角为θ的斜面上，最多能码多少块？

解：三力共点知识应用。

答： 。

4、两根等长的细线，一端拴在同一悬点O上，另一端各系一个小球，两球的质量分别为m1和m2 ，已知两球间存在大小相等、方向相反的斥力而使两线张开一定角度，分别为45和30°，如图15所示。则m1 : m2??为多少？

解说：本题考查正弦定理、或力矩平衡解静力学问题。

对两球进行受力分析，并进行矢量平移，如图16所示。

首先注意，图16中的灰色三角形是等腰三角形，两底角相等，设为α。

而且，两球相互作用的斥力方向相反，大小相等，可用同一字母表示，设为F 。

对左边的矢量三角形用正弦定理，有：

 =          ①

同理，对右边的矢量三角形，有： =                                ②

解①②两式即可。

答案：1 ： 。

（学生活动）思考：解本题是否还有其它的方法？

答：有——将模型看成用轻杆连成的两小球，而将O点看成转轴，两球的重力对O的力矩必然是平衡的。这种方法更直接、简便。

应用：若原题中绳长不等，而是l1 ：l2 = 3 ：2 ，其它条件不变，m1与m2的比值又将是多少？

解：此时用共点力平衡更加复杂（多一个正弦定理方程），而用力矩平衡则几乎和“思考”完全相同。

答：2 ：3 。

5、如图17所示，一个半径为R的均质金属球上固定着一根长为L的轻质细杆，细杆的左端用铰链与墙壁相连，球下边垫上一块木板后，细杆恰好水平，而木板下面是光滑的水平面。由于金属球和木板之间有摩擦（已知摩擦因素为μ），所以要将木板从球下面向右抽出时，至少需要大小为F的水平拉力。试问：现要将木板继续向左插进一些，至少需要多大的水平推力？

解说：这是一个典型的力矩平衡的例题。

以球和杆为对象，研究其对转轴O的转动平衡，设木板拉出时给球体的摩擦力为f ，支持力为N ，重力为G ，力矩平衡方程为：

f R + N（R + L）= G（R + L）           ①

球和板已相对滑动，故：f = μN        ②

解①②可得：f = 

再看木板的平衡，F = f 。

同理，木板插进去时，球体和木板之间的摩擦f′=  = F′。

答案： 。

第四讲 摩擦角及其它

一、摩擦角

1、全反力：接触面给物体的摩擦力与支持力的合力称全反力，一般用R表示，亦称接触反力。

2、摩擦角：全反力与支持力的最大夹角称摩擦角，一般用φm表示。

此时，要么物体已经滑动，必有：φm = arctgμ（μ为动摩擦因素），称动摩擦力角；要么物体达到最大运动趋势，必有：φms = arctgμs（μs为静摩擦因素），称静摩擦角。通常处理为φm = φms 。

3、引入全反力和摩擦角的意义：使分析处理物体受力时更方便、更简捷。

二、隔离法与整体法

1、隔离法：当物体对象有两个或两个以上时，有必要各个击破，逐个讲每个个体隔离开来分析处理，称隔离法。

在处理各隔离方程之间的联系时，应注意相互作用力的大小和方向关系。

2、整体法：当各个体均处于平衡状态时，我们可以不顾个体的差异而讲多个对象看成一个整体进行分析处理，称整体法。

应用整体法时应注意“系统”、“内力”和“外力”的涵义。

三、应用

1、物体放在水平面上，用与水平方向成30°的力拉物体时，物体匀速前进。若此力大小不变，改为沿水平方向拉物体，物体仍能匀速前进，求物体与水平面之间的动摩擦因素μ。

解说：这是一个能显示摩擦角解题优越性的题目。可以通过不同解法的比较让学生留下深刻印象。

法一，正交分解。（学生分析受力→列方程→得结果。）

法二，用摩擦角解题。

引进全反力R ，对物体两个平衡状态进行受力分析，再进行矢量平移，得到图18中的左图和中间图（注意：重力G是不变的，而全反力R的方向不变、F的大小不变），φm指摩擦角。

再将两图重叠成图18的右图。由于灰色的三角形是一个顶角为30°的等腰三角形，其顶角的角平分线必垂直底边……故有：φm = 15°。

最后，μ= tgφm 。

答案：0.268 。

（学生活动）思考：如果F的大小是可以选择的，那么能维持物体匀速前进的最小F值是多少？

解：见图18，右图中虚线的长度即Fmin ，所以，Fmin = Gsinφm 。

答：Gsin15°（其中G为物体的重量）。

2、如图19所示，质量m = 5kg的物体置于一粗糙斜面上，并用一平行斜面的、大小F = 30N的推力推物体，使物体能够沿斜面向上匀速运动，而斜面体始终静止。已知斜面的质量M = 10kg ，倾角为30°，重力加速度g = 10m/s2 ，求地面对斜面体的摩擦力大小。

解说：

本题旨在显示整体法的解题的优越性。

法一，隔离法。简要介绍……

法二，整体法。注意，滑块和斜面随有相对运动，但从平衡的角度看，它们是完全等价的，可以看成一个整体。

做整体的受力分析时，内力不加考虑。受力分析比较简单，列水平方向平衡方程很容易解地面摩擦力。

答案：26.0N 。

（学生活动）地面给斜面体的支持力是多少？

解：略。

答：135N 。

应用：如图20所示，一上表面粗糙的斜面体上放在光滑的水平地面上，斜面的倾角为θ。另一质量为m的滑块恰好能沿斜面匀速下滑。若用一推力F作用在滑块上，使之能沿斜面匀速上滑，且要求斜面体静止不动，就必须施加一个大小为P = 4mgsinθcosθ的水平推力作用于斜面体。使满足题意的这个F的大小和方向。

解说：这是一道难度较大的静力学题，可以动用一切可能的工具解题。

法一：隔离法。

由第一个物理情景易得，斜面于滑块的摩擦因素μ= tgθ

对第二个物理情景，分别隔离滑块和斜面体分析受力，并将F沿斜面、垂直斜面分解成Fx和Fy ，滑块与斜面之间的两对相互作用力只用两个字母表示（N表示正压力和弹力，f表示摩擦力），如图21所示。

对滑块，我们可以考查沿斜面方向和垂直斜面方向的平衡——

Fx = f + mgsinθ

Fy + mgcosθ= N

且 f = μN = Ntgθ

综合以上三式得到：

Fx = Fytgθ+ 2mgsinθ               ①

对斜面体，只看水平方向平衡就行了——

P = fcosθ+ Nsinθ

即：4mgsinθcosθ=μNcosθ+ Nsinθ

代入μ值，化简得：Fy = mgcosθ      ②

②代入①可得：Fx = 3mgsinθ

最后由F =解F的大小，由tgα= 解F的方向（设α为F和斜面的夹角）。

答案：大小为F = mg，方向和斜面夹角α= arctg()指向斜面内部。

法二：引入摩擦角和整体法观念。

仍然沿用“法一”中关于F的方向设置（见图21中的α角）。

先看整体的水平方向平衡，有：Fcos(θ- α) = P                                   ⑴

再隔离滑块，分析受力时引进全反力R和摩擦角φ，由于简化后只有三个力（R、mg和F），可以将矢量平移后构成一个三角形，如图22所示。

在图22右边的矢量三角形中，有： = =      ⑵

注意：φ= arctgμ= arctg(tgθ) = θ                                              ⑶

解⑴⑵⑶式可得F和α的值。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网