题目内容
11. 在真空中同一条直线上的A、B两点固定有电荷量分别为+4Q和-Q的点电荷,相距为L.求:
在真空中同一条直线上的A、B两点固定有电荷量分别为+4Q和-Q的点电荷,相距为L.求:(1)将另一个点电荷放在该直线上的哪个位置,可以使它在电场力作用下保持静止?
(2)若要求这三个点电荷都只在电场力作用下保持静止,那么引入的这个点电荷应是正电荷还是负电荷?电荷量是多大?
分析 三个点电荷都处于静止状态,对电荷受力分析,每个电荷都处于受力平衡状态,故根据库仑定律可分别对任意两球进行分析列出平衡方程即可求得结果
解答 解:①A、B两点的电荷是固定的,故将另一个点电荷放在该直线上的合场强为零的位置,可以使它在电场力作用下保持静止.
所以合场强为零的位置应该在-Q的外侧,设AB间距离为r,合场强为零的点在B的外侧,距离B为x,
则:EA=EB
所以$\frac{4kQ}{(r+x)^{2}}=\frac{kQ}{{x}^{2}}$
解得x=r
故第三个电荷在-Q的外侧,距离-Q的距离等于-Q距离+4Q的距离.
②三个电荷要平衡,必须三个电荷在一条直线上,外侧二个电荷相互排斥,中间电荷吸引外侧两个电荷,
所以外侧两个电荷距离大,要平衡中间电荷的拉力,必须外侧电荷电量大,中间电荷电量小,所以有“两大夹一小,两同夹一异”的结论.
所以第三个电荷必须为正电,在-Q的外侧,且为正电荷.
设AB间距离为r,引入点电荷在B的外侧,距离B为x,设引入的电荷的电荷量为q,
对B电荷,根据平衡条件有:$k\frac{4{Q}^{2}}{{r}^{2}}=k\frac{Qq}{{x}^{2}}$
对引入的电荷,根据平衡条件有:$k\frac{4{Q}^{2}}{{(r+x)}^{2}}=k\frac{Qq}{{x}^{2}}$
解得:$q=(\frac{r+x}{r})^{2}Q$=4Q,所以引入的这个点电荷的电荷量与位置有关.
答:①第三个电荷在-Q的外侧,距-Q的距离等于-Q距+4Q的距离.
②若要求这三个点电荷都只在电场力作用下保持静止,那么引入的这个点电荷应是正电荷,电荷量的大小4Q,其中AB间距离为r,引入点电荷在B的外侧,距离B为x.
点评 我们可以去尝试假设第三个电荷带正电或负电,它应该放在什么地方,能不能使整个系统处于平衡状态.不行再继续判断

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案| A. | 在研究郭晶晶跳水比赛中的动作要领时不能把郭晶晶看成质点 | |
| B. | 在研究物体的运动时参考系必须选地面或相对于地面静止不动的其他物体 | |
| C. | 列车时刻表上的数字如2:00指的是时刻而不是时间 | |
| D. | 如果两个质点在运动中通过路程相等,它们的位移大小一定相等 |
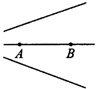
| A. | Q为负电荷时,电场强度EA>EB | B. | Q为负电荷时,电场强度EA<EB | ||
| C. | Q为正电荷时,电场强度EA>EB | D. | Q为正电荷时,电场强度EA<EB |
 一矩形线圈,在匀强磁场中绕垂直于磁场方向并位于线圈平面内的固定轴转动,线圈中的感应电动势e 随时间t的变化规律如图所示,则下列说法正确的是( )
一矩形线圈,在匀强磁场中绕垂直于磁场方向并位于线圈平面内的固定轴转动,线圈中的感应电动势e 随时间t的变化规律如图所示,则下列说法正确的是( )| A. | t1和t3时刻,穿过线圈的磁通量为零 | |
| B. | t1和t3时刻,穿过线圈的磁通量最大 | |
| C. | t=0时刻,线圈平面与磁场方向平行 | |
| D. | 当感应电动势e方向改变时,穿过线圈的磁通量最小 |
| A. | 6m-4m | B. | 4m lm | C. | 5m 0 | D. | 6m 4m |
 某次实验中得到一条如图所示的纸带,图中前几个点模糊,因此从A开始每打5个计时点取着为1个计数点,计时器打点频率为50Hz.则从打A点到打E点共历时0.4s,打D点时的瞬时速度是0.21m/s.
某次实验中得到一条如图所示的纸带,图中前几个点模糊,因此从A开始每打5个计时点取着为1个计数点,计时器打点频率为50Hz.则从打A点到打E点共历时0.4s,打D点时的瞬时速度是0.21m/s. 如图所示电路,R1=1Ω,R2=2Ω,R3=3Ω,a、b间电压为5V.当S断开时,c、d间电压为2V,当S闭合时,c、d间电压为0V.
如图所示电路,R1=1Ω,R2=2Ω,R3=3Ω,a、b间电压为5V.当S断开时,c、d间电压为2V,当S闭合时,c、d间电压为0V.