题目内容
2.某探测飞船以速度v绕某行星表面做匀速圆周运动,测得其运动的周期为T,已知引力常量为G,由此可以得到( )| A. | 该行星的半径为$\frac{vT}{π}$ | B. | 该行星的质量为$\frac{T{v}^{3}}{πG}$ | ||
| C. | 该行星的平均密度为$\frac{3π}{G{T}^{2}}$ | D. | 该行星表面的重力加速度为$\frac{vπ}{T}$ |
分析 近地飞行的飞船轨道半径等于行星的轨道半径,根据万有引力提供圆周运动的向心力可以求出行星的质量,该行星表面的重力加速度即为近地飞行飞船的向心加速度.
解答 解:A、根据圆周运动的周期与线速度的关系有T=$\frac{2πr}{v}$,所以该行星的半径r=$\frac{vT}{2π}$,故A错误;
B、万有引力提供向心力,$\frac{GMm}{{r}^{2}}$=m$\frac{{4π}^{2}}{{T}^{2}}$r
r=$\frac{vT}{2π}$,
可得该行星的质量为:M=$\frac{{v}^{3}T}{2πG}$,故B错误;
C、该行星的平均密度ρ=$\frac{M}{\frac{4{πR}^{3}}{3}}$=$\frac{3π}{G{T}^{2}}$,故C正确;
D、该星球表面自由落体加速度即为近地飞船的向心加速度,所以有:a=$\frac{{v}^{2}}{r}$=$\frac{2πv}{T}$,故D错误.
故选:C
点评 掌握近地飞行的航天器由万有引力提供向心力,能据此计算中心天体的质量是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.下列现象,哪些是因液体的表面张力所造成的( )
| A. | 宇宙飞船中,一大滴水银会成球状 | |
| B. | 熔化的蜡烛从燃烧的蜡烛上流下来,冷却后呈球形 | |
| C. | 熔融的玻璃可制成各种玻璃器皿 | |
| D. | 飘浮在热菜汤表面上的油滴,从上面观察是圆形的 |
10.木星公转周期约为12年,地球到太阳的距离为1天文单位,则木星到太阳的距离最接近( )
| A. | 5天文单位 | B. | 12天文单位 | C. | 2天文单位 | D. | 4天文单位 |
17.以初速度V0竖直上抛一个质量为M的物体,物体上升过程中所受阻力F大小不变,上升最大高度为H,则抛出过程中人对物体做的功( )
| A. | $\frac{1}{2}$MV02+MgH | B. | MgH | C. | $\frac{1}{2}$MV02 | D. | MgH+FH |
7.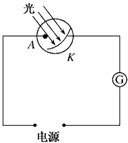 如图所示电路的全部接线及元件均完好.用光照射光电管的K极板,发现电流计无电流通过,可能的原因是( )
如图所示电路的全部接线及元件均完好.用光照射光电管的K极板,发现电流计无电流通过,可能的原因是( )
 如图所示电路的全部接线及元件均完好.用光照射光电管的K极板,发现电流计无电流通过,可能的原因是( )
如图所示电路的全部接线及元件均完好.用光照射光电管的K极板,发现电流计无电流通过,可能的原因是( )| A. | A、K间加的电压不够高 | B. | 电源正负极接反了 | ||
| C. | 照射光的强度不够大 | D. | 照射光的频率不够高 |
14.如图所示小物体A与圆盘保持相对静止跟着圆盘一起做匀速圆周运动,则下列说法正确的是( )
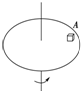

| A. | 木块受到圆盘对它的静摩擦力,方向指向圆盘中心 | |
| B. | 由于木块相对圆盘静止,所以不受摩擦力 | |
| C. | 由于木块运动,所以受到滑动摩擦力 | |
| D. | 由于木块做匀速圆周运动,所以,除了受到重力、支持力、摩擦力外,还受向心力 |
11.川师附中建设新的体育馆,需要用起重机把建筑材料运送到高处,一起重机的钢绳由静止开始匀加速提起质量为m的建筑材料,当重物的速度为v1时,起重机的有用功率达到最大值P,此后,起重机保持该功率不变,继续提升重物,直到以最大速度v2匀速上升为止,物体上升的高度为h,则整个过程中,下列说法正确的是( )
| A. | 钢绳的最大拉力为$\frac{P}{v_2}$ | B. | 钢绳的最大拉力为$\frac{P}{v_1}$ | ||
| C. | 重物的匀加速最大速度v1=$\frac{P}{mg}$ | D. | 起重机对重物做的功为mgh+$\frac{1}{2}$mv22 |
12. 如图所示,T为理想变压器,原副线圈匝数比为5:1.A1、A2为理想交流电流表,V1、V2为理想交流电压表,R1、R2为定值电阻,R3为光敏电阻(阻值随光照强度的增大而减小),原线圈两端电压u=220$\sqrt{2}$sin314tV,以下说法正确的是( )
如图所示,T为理想变压器,原副线圈匝数比为5:1.A1、A2为理想交流电流表,V1、V2为理想交流电压表,R1、R2为定值电阻,R3为光敏电阻(阻值随光照强度的增大而减小),原线圈两端电压u=220$\sqrt{2}$sin314tV,以下说法正确的是( )
 如图所示,T为理想变压器,原副线圈匝数比为5:1.A1、A2为理想交流电流表,V1、V2为理想交流电压表,R1、R2为定值电阻,R3为光敏电阻(阻值随光照强度的增大而减小),原线圈两端电压u=220$\sqrt{2}$sin314tV,以下说法正确的是( )
如图所示,T为理想变压器,原副线圈匝数比为5:1.A1、A2为理想交流电流表,V1、V2为理想交流电压表,R1、R2为定值电阻,R3为光敏电阻(阻值随光照强度的增大而减小),原线圈两端电压u=220$\sqrt{2}$sin314tV,以下说法正确的是( )| A. | 当光照增强时,电压表V1示数为44$\sqrt{2}$V保持不变 | |
| B. | 当光照增强时,电压表V2示数变大 | |
| C. | 通过电流表A1的电流方向每秒变化50次 | |
| D. | 当光照增强时,电流表A1、A2示数同时变大 |