题目内容
12.某星球的质量为M,半径为R.若万有引力恒量为G,且忽略该星球的自转,则该星球的表面重力加速度 g=$\frac{GM}{{R}^{2}}$.分析 在星球表面,忽略该星球的自转时,重力等于万有引力,根据万有引力定律列式求解即可.
解答 解:在星球表面,忽略该星球的自转时,重力等于万有引力,故:
mg=G$\frac{Mm}{{R}^{2}}$
解得:
g=$\frac{GM}{{R}^{2}}$
故答案为:$\frac{GM}{{R}^{2}}$.
点评 本题关键是明确在星球表面,重力和万有引力的联系,然后结合万有引力列式求解,基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.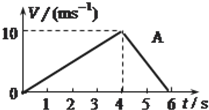 在平直公路上,汽车由静止开始做匀加速运动,当速度达到10m/s后立即关闭发动机直到停止,v-t图象如图所示,全过程中牵引力做功W1,克服摩擦力做功W2,则W1:W2为( )
在平直公路上,汽车由静止开始做匀加速运动,当速度达到10m/s后立即关闭发动机直到停止,v-t图象如图所示,全过程中牵引力做功W1,克服摩擦力做功W2,则W1:W2为( )
 在平直公路上,汽车由静止开始做匀加速运动,当速度达到10m/s后立即关闭发动机直到停止,v-t图象如图所示,全过程中牵引力做功W1,克服摩擦力做功W2,则W1:W2为( )
在平直公路上,汽车由静止开始做匀加速运动,当速度达到10m/s后立即关闭发动机直到停止,v-t图象如图所示,全过程中牵引力做功W1,克服摩擦力做功W2,则W1:W2为( )| A. | 1:1 | B. | 1:2 | C. | 1:3 | D. | 1:4 |
7.探月工程三期飞行试验器于2014年10月24日2时在中国西昌卫星发射中心发射升空,飞行试验器飞抵距月球6万千米附近进入月球引力影响区,开始在月球近旁转向飞行,最终进入距月球表面h=200km的圆形工作轨道.设月球半径为R,月球表面的重力加速度为g,万有引力常量为G,则下列选项错误的是( )
| A. | 飞行试验器在工作轨道上的绕行速度为R$\sqrt{\frac{g}{R+h}}$ | |
| B. | 飞行试验器工作轨道处的重力加速度为($\frac{R}{R+h}$)2g | |
| C. | 飞行试验器绕月球运行的周期为2π$\sqrt{\frac{R}{g}}$ | |
| D. | 月球的平均密度为$\frac{3g}{4πGR}$ |
4.关于功和能,下列说法中错误的是( )
| A. | 做了多少功,就有多少能量发生了变化 | |
| B. | 做功的过程就是物体能量的转化过程 | |
| C. | 功和能的单位相同,它们的物理意义也相同 | |
| D. | 各种不同形式的能量可以互相转化,而且在转化过程中能量总量保持不变 |
1.下列关于位移和路程的说法错误的是( )
| A. | 质点运动的位移大小可能大于路程 | |
| B. | 质点通过一段路程,其位移可能为零 | |
| C. | 沿直线运动的物体,位移的大小和路程有可能相等 | |
| D. | 质点沿不同的路径由A到B,其路程可能不同而位移是相同的 |
2.某探测飞船以速度v绕某行星表面做匀速圆周运动,测得其运动的周期为T,已知引力常量为G,由此可以得到( )
| A. | 该行星的半径为$\frac{vT}{π}$ | B. | 该行星的质量为$\frac{T{v}^{3}}{πG}$ | ||
| C. | 该行星的平均密度为$\frac{3π}{G{T}^{2}}$ | D. | 该行星表面的重力加速度为$\frac{vπ}{T}$ |