题目内容
15.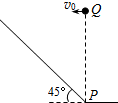 如图所示是倾角为45°的斜坡,在斜坡底端P点正上方某一位置Q处以速度v0水平向左抛出一个小球A,小球恰好能垂直落在斜坡上,运动时间为t1.小球B从同一点Q处自由下落,下落至P点的时间为t2,不计空气阻力,则t1:t2为( )
如图所示是倾角为45°的斜坡,在斜坡底端P点正上方某一位置Q处以速度v0水平向左抛出一个小球A,小球恰好能垂直落在斜坡上,运动时间为t1.小球B从同一点Q处自由下落,下落至P点的时间为t2,不计空气阻力,则t1:t2为( )| A. | 1:2 | B. | 1:$\sqrt{3}$ | C. | 1:3 | D. | 1:$\sqrt{2}$ |
分析 小球做平抛运动时,根据分位移公式求出竖直分位移和水平分位移之比,然后根据几何关系求解出的自由落体运动的位移并求出时间.
解答 解:小球A恰好能垂直落在斜坡上,如图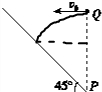
由几何关系可知,小球竖直方向的速度增量
vy=gt1=v0 ①
水平位移 S=v0t1 ②
竖直位移 hQ=$\frac{1}{2}g{t}_{1}^{2}$ ③
由①②③得到:$\frac{{h}_{Q}}{S}$=$\frac{1}{2}$
由几何关系可知小球B作自由下落的高度为:
hQ+S=$\frac{1}{2}g{t}_{2}^{2}$ ④
联立以上各式解得:$\frac{{t}_{1}}{{t}_{2}}$=$\frac{1}{\sqrt{3}}$
故选:B.
点评 本题关键是明确小球Q的运动是平抛运动,然后根据平抛运动的分位移和分速度公式联立求解出运动时间,再根据几何关系得到自由落体的位移,从而进一步求得时间,最后得到比值.

练习册系列答案
相关题目
9.下列关于匀速圆周运动的说法中,正确的是( )
| A. | 是线速度不变的运动 | B. | 是相对圆心位移不变的运动 | ||
| C. | 是角速度不断变化的运动 | D. | 是角速度不变的运动 |
10.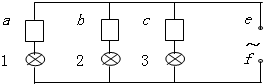 如图所示,在e、f间接上交流电源,保持电压最大值不变,使其频率增大,发现各灯的亮度变化情况是:灯1变暗,灯2变亮,灯3不变.则黑箱a、b、c中所接元件可能是( )
如图所示,在e、f间接上交流电源,保持电压最大值不变,使其频率增大,发现各灯的亮度变化情况是:灯1变暗,灯2变亮,灯3不变.则黑箱a、b、c中所接元件可能是( )
 如图所示,在e、f间接上交流电源,保持电压最大值不变,使其频率增大,发现各灯的亮度变化情况是:灯1变暗,灯2变亮,灯3不变.则黑箱a、b、c中所接元件可能是( )
如图所示,在e、f间接上交流电源,保持电压最大值不变,使其频率增大,发现各灯的亮度变化情况是:灯1变暗,灯2变亮,灯3不变.则黑箱a、b、c中所接元件可能是( )| A. | a为电阻,b为电容器,c为电感线圈 | B. | a为电阻,b为电感线圈,c为电容器 | ||
| C. | a为电容器,b为电感线圈,c为电阻 | D. | a为电感线圈,b为电容器,c为电阻 |
3.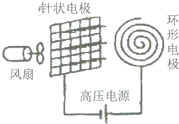 空气中的负离子对人的健康极为有益,人工产生负离子的最常见方法是电晕放电法.如图所示,一排针状负极和环形正极之间加上直流高压电,电压达5000V左右,使空气发生电离,从而产生一价的负氧离子排出,使空气清新化,针状负极与环形正极间距为5mm,且视为匀强电场,电子电量e=1.60×10-19C;若电场强度为E,电场对负氧离子的作用力为F,则 ( )
空气中的负离子对人的健康极为有益,人工产生负离子的最常见方法是电晕放电法.如图所示,一排针状负极和环形正极之间加上直流高压电,电压达5000V左右,使空气发生电离,从而产生一价的负氧离子排出,使空气清新化,针状负极与环形正极间距为5mm,且视为匀强电场,电子电量e=1.60×10-19C;若电场强度为E,电场对负氧离子的作用力为F,则 ( )
 空气中的负离子对人的健康极为有益,人工产生负离子的最常见方法是电晕放电法.如图所示,一排针状负极和环形正极之间加上直流高压电,电压达5000V左右,使空气发生电离,从而产生一价的负氧离子排出,使空气清新化,针状负极与环形正极间距为5mm,且视为匀强电场,电子电量e=1.60×10-19C;若电场强度为E,电场对负氧离子的作用力为F,则 ( )
空气中的负离子对人的健康极为有益,人工产生负离子的最常见方法是电晕放电法.如图所示,一排针状负极和环形正极之间加上直流高压电,电压达5000V左右,使空气发生电离,从而产生一价的负氧离子排出,使空气清新化,针状负极与环形正极间距为5mm,且视为匀强电场,电子电量e=1.60×10-19C;若电场强度为E,电场对负氧离子的作用力为F,则 ( )| A. | E=1O3N/C,F=1.6×10-l6N | B. | E=106N/C,F=1.6×10-16N | ||
| C. | E=103N/C,F=1.6×10-13N | D. | E=106N/C,F=1.6×l0-13N |
10.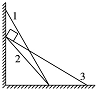 将三个木板1、2、3固定在墙角,木板与墙壁和地面构成了三个不同的三角形,如图所示,其中1与2底边相同,2和3高度相同.现将一个可视为质点的物块分别从三个木板的顶端由静止释放,并沿木板下滑到底端,物块与木板之间的动摩擦因数μ均相同.在这三个过程中,下列说法正确的是( )
将三个木板1、2、3固定在墙角,木板与墙壁和地面构成了三个不同的三角形,如图所示,其中1与2底边相同,2和3高度相同.现将一个可视为质点的物块分别从三个木板的顶端由静止释放,并沿木板下滑到底端,物块与木板之间的动摩擦因数μ均相同.在这三个过程中,下列说法正确的是( )
 将三个木板1、2、3固定在墙角,木板与墙壁和地面构成了三个不同的三角形,如图所示,其中1与2底边相同,2和3高度相同.现将一个可视为质点的物块分别从三个木板的顶端由静止释放,并沿木板下滑到底端,物块与木板之间的动摩擦因数μ均相同.在这三个过程中,下列说法正确的是( )
将三个木板1、2、3固定在墙角,木板与墙壁和地面构成了三个不同的三角形,如图所示,其中1与2底边相同,2和3高度相同.现将一个可视为质点的物块分别从三个木板的顶端由静止释放,并沿木板下滑到底端,物块与木板之间的动摩擦因数μ均相同.在这三个过程中,下列说法正确的是( )| A. | 沿着1和2下滑到底端时,物块速度的大小不相等;沿着2和3下滑到底端时,物块速度的大小相等 | |
| B. | 沿着1下滑到底端时,物块的速率最大 | |
| C. | 物块沿着3下滑到底端的过程中,产生的热量是最多的 | |
| D. | 物块沿着1和2下滑到底端的过程中,产生的热量是一样多 |
20.下列说法正确的是( )
| A. | Th核发生一次α衰变时,新核与原来的原子核相比,中子数减少了4 | |
| B. | 太阳辐射的能量主要来自太阳内部的热核反应 | |
| C. | 若使放射性物质的温度升高,其半衰期可能变小 | |
| D. | 用14eV的光子照射处于基态的氢原子,可使其电离 | |
| E. | 汤姆孙发现了电子,并提出了原子的枣糕模型 |
7.下列物理量的单位中,属于国际单位制中的基本单位的是( )
| A. | 牛顿 | B. | 秒 | C. | 焦耳 | D. | 瓦 |
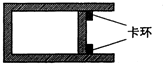 如图所示,一内壁光滑的气缸固定于水平地面上,在距气缸底部L=54cm处有一固定于气缸上的卡环,活塞与气缸底部之间封闭着一定质量的理想气体,活塞在图示位置时封闭气体的温度t1=267℃,压强p1=1.5atm.设大气压强ρ0恒为1atm,气缸导热性能良好,不计活塞的厚度.由于气缸缓慢放热,活塞最终会左移到某一位置而平衡.求
如图所示,一内壁光滑的气缸固定于水平地面上,在距气缸底部L=54cm处有一固定于气缸上的卡环,活塞与气缸底部之间封闭着一定质量的理想气体,活塞在图示位置时封闭气体的温度t1=267℃,压强p1=1.5atm.设大气压强ρ0恒为1atm,气缸导热性能良好,不计活塞的厚度.由于气缸缓慢放热,活塞最终会左移到某一位置而平衡.求