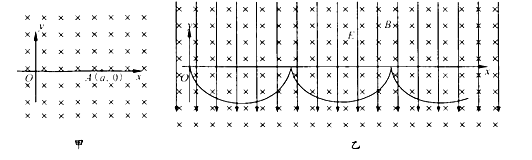
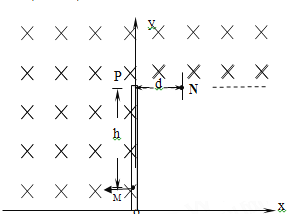
[题目]如图.xoy平面内y轴上OP间有绝缘弹性竖直档板.在第一象限有一点N, PN间距离d=3m.第二象限以及第一象限PN连线上方存在匀强磁场.磁场方向垂直纸面向里.磁感应强度B=1T.挡板下端附近M点有一粒子源.PM之间的距离h=9m, 粒子源可以沿x轴负方向发射速度不同带电粒子.粒子质量m=1.0×10-12kg.电量q=-1.0×10-6 C 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，xoy平面内y轴上OP间有绝缘弹性竖直档板，在第一象限有一点N, PN间距离d=3m。第二象限以及第一象限PN连线上方存在匀强磁场，磁场方向垂直纸面向里，磁感应强度B=1T。挡板下端附近M点有一粒子源，PM之间的距离h=9m, 粒子源可以沿x轴负方向发射速度不同带电粒子，粒子质量m=1.0×10-12kg，电量q=-1.0×10-6 C。粒子若与档板相碰将原速率弹回，且碰撞时间不计，碰撞时电量不变，最后有一些粒子能从N点离开磁场。不计粒子重力和粒子间的相互作用。关于这些从N点离开磁场的粒子，下列说法正确的是( )

A. 粒子速度对应值可以有无数个 B. 粒子运动的最长时间是

C. 半径R=3.75m的粒子运动时间最长 D. 速度为5×10-6m/s的粒子半径最大

【答案】CD

【解析】设粒子做圆周运动的半径为r，当粒子经过N点时，由几何关系需满足，其中n=0,1,2,3……计算可知n只能取0，1式子才有解；选项A错误；

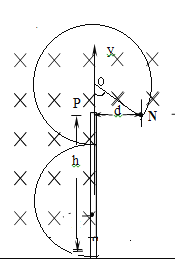
当n=0时，解得r0=5m；当n=1时，r1=3m，r2=；当r2=时粒子在磁场中运动的时间最长，粒子的周期为；粒子对应的速度转过的角度为，则对应的时间，选项B错误，C正确；当n=0时，解得r0=5m；此时粒子的半径最大，根据可知，，选项D正确；故选CD.

练习册系列答案

A. 摩擦力Ff逐渐增大

B. 摩擦力Ff先增大后减小

C. 支持力FN逐渐增大

D. 支持力FN先减小后不变

【题目】地球的两颗人造卫星质量之比m1：m2=1：2，圆周运动轨道半径之比r1：r2=1：2，则 ( )

A. 它们的线速度之比为v1：v2= B. 它们的运动周期之比为T1：T2=

C. 它们的向心加速度之比为a1：a2=4：1 D. 它们的向心力之比为F1：F2=4：1

【题目】如图所示，矩形abcd长ad=0.6m，宽ab=0.3m，O、e分别是ad、bc的中点，以O为圆心Oa为半径的半圆形区域内有垂直纸面向里的匀强磁场，磁感应强度B=0.25T。一群不计重力、质量m=3×10-7kg、电量q=2×10-3C的正电荷以速度v=5×102m/s沿平行于ab方向且垂直于磁场射入磁场区域，则下列判断正确的是

A. 从be间射入的粒子，出射点都分布在Oa边

B. 从ce间射入的粒子，均从d点离开磁场

C. 从ce间射入的粒子中，通过磁场的最长时间为

D. 从ce间射入的所有粒子，通过磁场区域的面积是

【题目】如图，一带有活塞的气缸通过底部的水平细管与一个上端封闭的竖直管相连，气缸和竖直管均导热，气缸与竖直管的横截面积之比为3：1，初始时，该装置底部盛有水银；左右两边均封闭有一定质量的理想气体，左边气柱高24cm，右边气柱高22cm；两边液面的高度差为4cm．竖直管内气体压强为76cmHg，现使活塞缓慢向下移动，使气缸和竖直管内的水银面高度相差8cm，活塞与气缸间摩擦不计．求

①此时竖直管内气体的压强；

②活塞向下移动的距离．

【题目】如图甲所示，空间存在一范围足够大、方向垂直于竖直xOy平面向里的匀强磁场，磁感应强度大小为B。让质量为m，电荷量为q（q>0）的粒子从坐标原点O沿xOy平面入射。不计粒子重力，重力加速度为g。

（1）若该粒子沿y轴负方向入射后，恰好能经过x轴上的A（a,0）点，求粒子速度的大小。

（2）若该粒子以速度v沿y轴负方向入射的同时，一不带电的小球从x轴上方某一点平行于x轴向右抛出，二者经过时恰好相遇，求小球抛出点的纵坐标。

（3）如图乙所示，在此空间再加入沿y轴负方向、大小为E的匀强电场，让该粒子改为从O点静止释放，研究表明：粒子在xOy平面内将做周期性运动，其周期，且在任一时刻，粒子速度的水平分量与其所在位置的y轴坐标绝对值的关系为。若在粒子释放的同时，另有一不带电的小球从x轴上方某一点平行于x轴向右抛出，二者经过时间恰好相遇，求小球抛出点的纵坐标。