题目内容
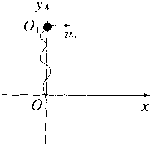 在光滑绝缘体竖直面上建立一直角坐标系,如图所示,一质量为m=1kg、电荷量为q的带正电小球,系于长为L=2m的不可伸长的弹性轻绳的一端,绳的另一端固定在坐标原点O,如图.现竖直平面上加一电场强度大小为E=3mg/q,方向沿y轴负方向的匀强电场,若把小球从O点的正上方距离O点1m处的O1点以速度v2=4
在光滑绝缘体竖直面上建立一直角坐标系,如图所示,一质量为m=1kg、电荷量为q的带正电小球,系于长为L=2m的不可伸长的弹性轻绳的一端,绳的另一端固定在坐标原点O,如图.现竖直平面上加一电场强度大小为E=3mg/q,方向沿y轴负方向的匀强电场,若把小球从O点的正上方距离O点1m处的O1点以速度v2=4| 5 |
(1)轻绳即将伸直时,绳与竖直方向的夹角为θ为多少?
(2)绳被拉直的瞬时,绳对小球所做的功;
(3)当小球再一次经过y轴的瞬时,绳对小球的拉力为多大?
分析:小球在复合场中注意分清小球的运动过程,轻绳即将伸直时,小球做类似平抛运动,根据平抛运动规律可求得绳与竖直方向的夹角;绳被拉直的瞬间,有能量损失,小球损失的能量即为绳对小球做的功;然后小球做圆周运动,由能量守恒求得小球到最低点的速度,根据向心力公式可求绳的拉力.
解答:解:(1)第一过程:小球做类似平抛运动,设绳子即将伸直时,绳子与竖直向上的方向的夹角为θ
如图所示:

v0t=Lsinθ
a=
=3g+g=4g
at2=
-Lcosθ,其中v0=4
m/s,L=2m
联立解得:θ=
(2)第二过程:绳绷直过程,绳绷直时,绳刚好水平,如下图所示: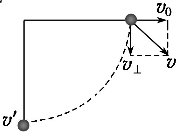
由于绳不可伸长,故绷直时,v0损失,小球仅有速度v⊥,且v⊥2=2×4g×
=4gL
小球损失的能量即为绳对小球做的功
W=0-
m
=-
m
代入数据,解得:W=-40J
(3)第三过程:小球在竖直平面内做圆周运动,设小球到达O点正下方时,速度为v′
根据能量守恒有:
mv′2=
m
+4mgL
设此时绳子对小球的拉力为F
则F-4mg=
联立可得:F=160N
答:(1)轻绳即将伸直时,绳与竖直方向的夹角为θ为
;(2)绳被拉直的瞬时,绳对小球所做的功为-40J;(3)当小球再一次经过y轴的瞬时,绳对小球的拉力为160N
如图所示:

v0t=Lsinθ
a=
| qE+mg |
| m |
| 1 |
| 2 |
| L |
| 2 |
| 5 |
联立解得:θ=
| π |
| 2 |
(2)第二过程:绳绷直过程,绳绷直时,绳刚好水平,如下图所示:

由于绳不可伸长,故绷直时,v0损失,小球仅有速度v⊥,且v⊥2=2×4g×
| L |
| 2 |
小球损失的能量即为绳对小球做的功
W=0-
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 0 |
代入数据,解得:W=-40J
(3)第三过程:小球在竖直平面内做圆周运动,设小球到达O点正下方时,速度为v′
根据能量守恒有:
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 ⊥ |
设此时绳子对小球的拉力为F
则F-4mg=
| mv′2 |
| L |
联立可得:F=160N
答:(1)轻绳即将伸直时,绳与竖直方向的夹角为θ为
| π |
| 2 |
点评:本题考查小球在复合场中的运动,关键要分清小球的运动过程,小球先做类平抛运动,绳绷直时有能量损失,然后做圆周运动,题目综合性较强,有一定的难度.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目