题目内容
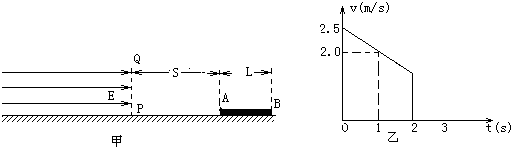
如图甲所示,水平面被竖直线PQ分为左右两部分,左部分光滑,范围足够大,上方存在水平向右的匀强电场.右部分粗糙,一质量为m=2kg,长为L的绝缘体制成的均匀带电的直棒AB置于水平面上,A端距PQ的距离为S=3m,给棒一个水平向左的初速v0,并以此时作为时间的起点,棒在最初2秒的运动图象如图乙所示.2秒末棒的B端刚好进入电场,已知直棒单位长度带电量为λ=0.1C/m,取重力加速度g=10m/s2.
求:(1)直棒的长度;(2)匀强电场的场强E;(3)直棒最终停在何处?
求:(1)直棒的长度;(2)匀强电场的场强E;(3)直棒最终停在何处?

分析:(1)根据图象求出2s内的位移,然后结合几何关系求出棒的长度;
(2)由图象可以知道物体加速度一直不变,说明物体全部进入电场时受到的电场力等于进入前的滑动摩擦力,根据平衡条件列式求解;
(3)棒在电场中静止时,电场力不为零,故不会一直不动,在电场外停下时,摩擦力减为零,不再运动.
(2)由图象可以知道物体加速度一直不变,说明物体全部进入电场时受到的电场力等于进入前的滑动摩擦力,根据平衡条件列式求解;
(3)棒在电场中静止时,电场力不为零,故不会一直不动,在电场外停下时,摩擦力减为零,不再运动.
解答:解:(1)由图信息可知棒加速度a=0.5m/s2,初速v0=2.5m/s,设棒2内秒位移为L1,则s=v0t-
at2=4m
而棒B端恰进电场,则棒长L=L1-S=1m
即直棒的长度为1m.
(2)由图可知棒进入电场后加速度不变,棒受到向右的电场力和减少的摩擦力应该相等.设棒进入电场x,则有
xλE=
mgμ 而 a=μg 所以 E=
=10N/C
即匀强电场的场强E为10N/C.
(3)棒全过程均做匀减速运动,B端恰进入电场时的速度V1,由图可知V1=1.5m/s.
穿出电场过程
-
L=
mv22-
mv12 得v2=1.5m/s
再返回至PQ处时仍为1.5m/s
所以继续滑行距离S2满足:2μgS2=V22 得S2=2.25m
所以直棒最终停下时,A端离PQ2.25m.
| 1 |
| 2 |
而棒B端恰进电场,则棒长L=L1-S=1m
即直棒的长度为1m.
(2)由图可知棒进入电场后加速度不变,棒受到向右的电场力和减少的摩擦力应该相等.设棒进入电场x,则有
xλE=
| x |
| L |
| mgμ |
| λL |
即匀强电场的场强E为10N/C.
(3)棒全过程均做匀减速运动,B端恰进入电场时的速度V1,由图可知V1=1.5m/s.
穿出电场过程
| λEL |
| 2 |
| mgμ |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
再返回至PQ处时仍为1.5m/s
所以继续滑行距离S2满足:2μgS2=V22 得S2=2.25m
所以直棒最终停下时,A端离PQ2.25m.
点评:本题关键根据图象,得到物体的运动情况,再通过受力分析,结合牛顿第二定律得出物体的受力情况,再进一步确定物体的运动情况.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目



