题目内容
3.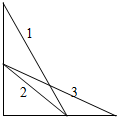 如图所示有三个斜面1、2、3,斜面1与2底边相同,斜面2和3高度相同,同一物体与三个斜面的动摩擦因数相同,他们分别沿三个斜面从顶端由静止下滑到底端,下列说法正确的是( )
如图所示有三个斜面1、2、3,斜面1与2底边相同,斜面2和3高度相同,同一物体与三个斜面的动摩擦因数相同,他们分别沿三个斜面从顶端由静止下滑到底端,下列说法正确的是( )| A. | 到达底端的速度v1=v2<v3 | |
| B. | 损失的机械能△E1=△E2>△E3 | |
| C. | 到达斜面底端时重力的瞬时功率P1>P2>P3 | |
| D. | 沿斜面运动的时间t1>t2>t3 |
分析 物体从斜面下滑过程中,重力做正功,摩擦力做负功,根据动能定理可以比较三者速度大小,注意物体在运动过程中克服摩擦力所做功等于因摩擦产生热量,据此可以比较重力的瞬时功率和运动时间.
解答 解:A、设物体滑到底端时的速度为v,根据动能定理得:
mgh-mgμLcosθ=$\frac{1}{2}m{V}^{2}$-0,根据图中斜面高度和底边长度可知滑到底边时速度大小关系为:v1>v2>v3,故A错误
B、设任一斜面和水平方向夹角为θ,斜面长度为L,则物体下滑过程中克服摩擦力做功为:Wf=mgμLcosθ.Lcosθ即为底边长度,由图可知1和2底边相等且小于3的,故有Wf1=Wf2<Wf3.根据功能关系有:Q=Wf,故摩擦生热关系为:Q1=Q2<Q3,损失的机械能△E1=△E2<△E3,故B错误;
C、设物体滑到底端时的速度为v,根据动能定理得:
mgh-mgμLcosθ=$\frac{1}{2}m{V}^{2}$-0,根据图中斜面高度和底边长度可知滑到底边时速度大小关系为:v1>v2>v3,
根据P=mgvcosα得,因为v1>v2>v3,α1<α2<α3,则重力做功的瞬时功率P1>P2>P3.故C正确
D、沿斜面运动的时间t=$\sqrt{\frac{2L}{gsinθ-μgcosθ}}$,θ2>θ3,L2<L3,所以t2<t3,由于动摩擦因数和斜面1、2的倾角关系未知,无法确定t1和t2,D错误.
故选:C
点评 本题比较简单直接利用功能关系即可求解,易错点在于写出表达式后的数学运算,因此学生要加强练习,提高利用数学知识解决物理问题的能力

练习册系列答案
相关题目
13.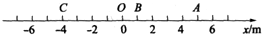 一个物体做直线运动,在物体运动所在的直线上建立如图所示的一维的直线坐标系,此物体从A运动到C,再从C运动到B.下列说法中正确的是( )
一个物体做直线运动,在物体运动所在的直线上建立如图所示的一维的直线坐标系,此物体从A运动到C,再从C运动到B.下列说法中正确的是( )
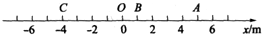 一个物体做直线运动,在物体运动所在的直线上建立如图所示的一维的直线坐标系,此物体从A运动到C,再从C运动到B.下列说法中正确的是( )
一个物体做直线运动,在物体运动所在的直线上建立如图所示的一维的直线坐标系,此物体从A运动到C,再从C运动到B.下列说法中正确的是( )| A. | 坐标轴上的坐标表示物体的位移 | |
| B. | 物体从A到C的位移可用坐标的变化量△x1=4m-5m=-1m表示 | |
| C. | C到B的位移△x2=5m大于A到C的位移△x1=-9m,因为正数大于负数 | |
| D. | 物体由A到B的合位移△x=1m-5m=-4m |
14.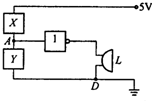 如图所示的电路图是一个应用“非”门构成一个简易火警报警电路,当热敏电阻的温度升高时,其阻值将变小,则图中X框、Y框中应是( )
如图所示的电路图是一个应用“非”门构成一个简易火警报警电路,当热敏电阻的温度升高时,其阻值将变小,则图中X框、Y框中应是( )
 如图所示的电路图是一个应用“非”门构成一个简易火警报警电路,当热敏电阻的温度升高时,其阻值将变小,则图中X框、Y框中应是( )
如图所示的电路图是一个应用“非”门构成一个简易火警报警电路,当热敏电阻的温度升高时,其阻值将变小,则图中X框、Y框中应是( )| A. | X为热敏电阻,Y为可变电阻 | B. | X 为热敏电阻,Y为开关 | ||
| C. | X为可变电阻,Y为热敏电阻 | D. | X、Y为热敏电阻 |
11.下列有关机械运动的说法中,错误的是( )
| A. | 宇宙中一切物质的运动是绝对的 | |
| B. | 太阳系中,只能说“地球绕太阳运动”,而不能说“太阳绕地球运动” | |
| C. | 我们日常说的运动和静止都是相对的,是相对于参考系而言的 | |
| D. | 若甲相对于乙是运动的,则乙相对于甲也是运动的 |
18.使用电磁打点计时器时,要注意到下面哪些问题 ( )
| A. | 先拉动纸带,后闭合电源打点 | |
| B. | 使用电压一定要控制在6V以上 | |
| C. | 要使用低压交流电源 | |
| D. | 纸带与打点计时器间摩擦力越大越好 |
12.一个做竖直上抛运动的物体,不计空气阻力时,上升过程中的平均速度是10m/s,则它能达到的最大高度为(取g=10m/s2)( )
| A. | 5 m | B. | 10 m | C. | 20 m | D. | 30 m |
13.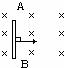 金属杆AB处于磁感强度B=1T的匀强磁场中,磁场方向垂直纸面向里.已知AB=20cm,当金属杆以速度v=10m/s按图中标明的方向运动时,则A、B两点间的电势差为( )
金属杆AB处于磁感强度B=1T的匀强磁场中,磁场方向垂直纸面向里.已知AB=20cm,当金属杆以速度v=10m/s按图中标明的方向运动时,则A、B两点间的电势差为( )
 金属杆AB处于磁感强度B=1T的匀强磁场中,磁场方向垂直纸面向里.已知AB=20cm,当金属杆以速度v=10m/s按图中标明的方向运动时,则A、B两点间的电势差为( )
金属杆AB处于磁感强度B=1T的匀强磁场中,磁场方向垂直纸面向里.已知AB=20cm,当金属杆以速度v=10m/s按图中标明的方向运动时,则A、B两点间的电势差为( )| A. | -2.0V | B. | 2.0V | C. | -200V | D. | 200V |
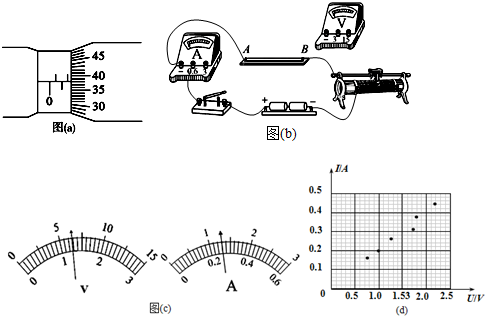
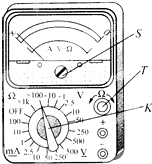 用如图所示的多用电表测量电阻,要用到选择开关K和两个部件S、T.请根据下列步骤完成电阻测量:
用如图所示的多用电表测量电阻,要用到选择开关K和两个部件S、T.请根据下列步骤完成电阻测量: