题目内容
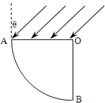 如图,空气中有一折射率为
如图,空气中有一折射率为| 2 |
分析:注意两条特殊光线,一是从O点沿半径方向进入玻璃柱体的光线,在AO面上折射后传播入方向不变,二是在AB面上发生全反射的光线,有光透出的部分在这两条光线之间,然后根据几何关系求解.
解答:解:A、根据折射定律有:
=
可得光进入玻璃后光线与竖直方向的夹角为30°.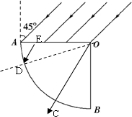
过O的光线垂直入射到AB界面上点C射出,C到B之间没有光线射出;越接近A的光线入射到AB界面上时的入射角越大,发生全反射的可能性越大.
根据临界角公式:sinC=
,得临界角为45°,如果AB界面上的临界点为D,此光线在AO界面上点E入射,在三角形ODE中可求得OD与水平方向的夹角为180°-(120°+45°)=15°,所以A到D之间没有光线射出.由此可得没有光线射出的圆弧对应圆心角为90°-(30°+15°)=45°
所以有光透出的部分的弧长为
.故A错误,B正确.
C、增大θ,则折射角也增大,根据几何关系,设折射角为α,则有光线射出的部分对应的圆心角为90°-α-(180°-135°-α)=45°,知对应的弧长不变.故C正确,D错误.
故选BC.
| sin45° |
| sinr |
| 2 |

过O的光线垂直入射到AB界面上点C射出,C到B之间没有光线射出;越接近A的光线入射到AB界面上时的入射角越大,发生全反射的可能性越大.
根据临界角公式:sinC=
| 1 | ||
|
所以有光透出的部分的弧长为
| πR |
| 4 |
C、增大θ,则折射角也增大,根据几何关系,设折射角为α,则有光线射出的部分对应的圆心角为90°-α-(180°-135°-α)=45°,知对应的弧长不变.故C正确,D错误.
故选BC.
点评:本题考查光的折射和全反射,意在考查正确地作出光路图解决几何光学问题的能力和综合运用知识的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,均匀玻璃中有一球形气泡,泡内为空气,球心为O.一束由两种色光混合而成的很细的复色光由PQ方向(PQ延长线不过圆心)从玻璃射入气泡中,经折射后分别从界面上的a、b两点射出(图中a、b两点未标出,已知a点比b点离直线PQ更远),则下列说法正确的是( )
如图,均匀玻璃中有一球形气泡,泡内为空气,球心为O.一束由两种色光混合而成的很细的复色光由PQ方向(PQ延长线不过圆心)从玻璃射入气泡中,经折射后分别从界面上的a、b两点射出(图中a、b两点未标出,已知a点比b点离直线PQ更远),则下列说法正确的是( ) 如图所示,空气中有一块横截面呈扇形的玻璃砖,玻璃砖的折射率为
如图所示,空气中有一块横截面呈扇形的玻璃砖,玻璃砖的折射率为 (2011?湖州模拟)如图所示,空气中有一块横截面呈扇形的玻璃砖,折射率为
(2011?湖州模拟)如图所示,空气中有一块横截面呈扇形的玻璃砖,折射率为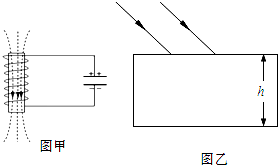 (1)有以下说法:
(1)有以下说法: 物理-选修-3-4
物理-选修-3-4