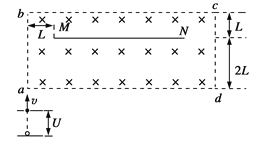
题目内容
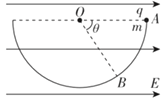
【题目】三个质量相等,分别带正电、负电和不带电的粒子,从带电平行金属板左侧中央以相同的水平初速度v0先后垂直电场进入,并分别落在正极板的A、B、C三处,O点是下极板的左端点,且OC=2OA,AC=2BC,如图所示,则下列说法正确的是( )
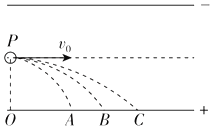
A. 三个粒子在电场中运动的时间之比tA:tB:tC=2:3:4
B. 三个粒子在电场中运动的加速度之比aA:aB:aC=1:3:4
C. 三个粒子在电场中运动时动能的变化量之比EkA:EkB:EkC=36:16:9
D. 带正、负电荷的两个粒子的电荷量之比为7:20
【答案】ACD
【解析】A、三个粒子的初速度相等,在水平方向上做匀速直线运动,由x=vt得,运动时间![]() ,故A正确;
,故A正确;
B、三个粒子在竖直方向上的位移y相等,根据![]() ,解得:
,解得:![]() ,故B错误;
,故B错误;
C、由牛顿第二定律可知F=ma,因为质量相等,所以合力之比与加速度之比相同,合力做功W=Fy,由动能定理可知,动能的变化量等于合力做的功,所以,三个粒子在电场中运动过程的动能变化量之比为![]() ,故C正确;
,故C正确;
D、三个粒子的合力大小关系为:![]() ,三个粒子的重力相等,所以B仅受重力作用,A所受的电场力向下,C所受的电场力向上,即B不带电,A带负电,C带正电,由牛顿第二定律得:
,三个粒子的重力相等,所以B仅受重力作用,A所受的电场力向下,C所受的电场力向上,即B不带电,A带负电,C带正电,由牛顿第二定律得:![]() ,解得:
,解得:![]() ,故D正确;
,故D正确;
故选ACD。

练习册系列答案
相关题目