题目内容
1.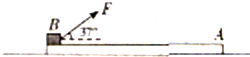 如图所示,质量mA=1kg、长L=6.0m的长板置于水平面上,质量mB=2kg的小滑块置于长板A的左端,A与水平面的动摩擦因数μ1=0.3,B与A间的动摩擦因数μ2=0.5,对B施加一大小为F=20N、方向与水平面成37°的恒力.最大静摩擦力等于滑动摩擦力,重力加速度g=10m/s2,sin37°=0.6.cos37°=0.8.
如图所示,质量mA=1kg、长L=6.0m的长板置于水平面上,质量mB=2kg的小滑块置于长板A的左端,A与水平面的动摩擦因数μ1=0.3,B与A间的动摩擦因数μ2=0.5,对B施加一大小为F=20N、方向与水平面成37°的恒力.最大静摩擦力等于滑动摩擦力,重力加速度g=10m/s2,sin37°=0.6.cos37°=0.8.(1)求A、B的加速度大小;
(2)若力F作用一段时间后,撤去力F,B能从A的左端滑到右端,求力F作用的最短时间.
分析 (1)分别对A和B进行受力分析,然后由牛顿第二定律即可求出加速度
(2)抓住B物体到达最右端时AB具有相同速度即可,此时作用力F最小,利用好运动学公式即可
解答 解:(1)A 对B的最大静摩擦力fB=μ2(mBg-Fsin37°)=4N
地面对A的摩擦力为fA=μ1(mAg+mBg-Fsin37°)=5.4N
故A静止,aA=0
对B力分析,由牛顿第二定律可得有:Fcosθ-fAB=mBaB
Fsinθ+NAB=mBg
fAB=μNAB
解得aB=6m/s2
(2)撤去外力F时,B的速度为v0,此后B做匀减速运动用时t2,若B到达A的右端时恰好与A具有共同速度v,则力F的作用时间为t1最短
B做匀减速运动的加速度${a}_{B1}={μ}_{2}g=5m/{s}^{2}$
A做加速运动的加速度为${a}_{A1}=\frac{{μ}_{2}{m}_{B}g-{μ}_{1}({m}_{A}+{m}_{B})g}{{m}_{A}}=1m/{s}^{2}$
v=v0-aB1t2
v=aA1t2
$\frac{{v}_{0}^{2}}{2{a}_{B}}+\frac{v+{v}_{0}}{2}{t}_{2}-\frac{v}{2}{t}_{2}=L$
力F作用的最短时间${t}_{1}=\frac{v}{{a}_{B}}$
联立解得t1=1s
答:(1)A、B的加速度大小分别为0,6m/s2;
(2)若力F作用一段时间后,撤去力F,B能从A的左端滑到右端,力F作用的最短时间为1s
点评 本题是牛顿第二定律和运动学公式的综合应用,要抓住两个物体运动的同时性和位移关系求解作用力F的最短时间

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.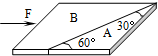 将某种材料的长方体锯成A、B两块放在水平桌面上,并紧靠在一起,如图所示,物体A的角度如图中所示.现用水平方向的力F推物体,使A、B保持矩形整体沿力F方向匀速运动,则( )
将某种材料的长方体锯成A、B两块放在水平桌面上,并紧靠在一起,如图所示,物体A的角度如图中所示.现用水平方向的力F推物体,使A、B保持矩形整体沿力F方向匀速运动,则( )
 将某种材料的长方体锯成A、B两块放在水平桌面上,并紧靠在一起,如图所示,物体A的角度如图中所示.现用水平方向的力F推物体,使A、B保持矩形整体沿力F方向匀速运动,则( )
将某种材料的长方体锯成A、B两块放在水平桌面上,并紧靠在一起,如图所示,物体A的角度如图中所示.现用水平方向的力F推物体,使A、B保持矩形整体沿力F方向匀速运动,则( )| A. | 物体A在水平方向受两个力作用,合力为零 | |
| B. | 作用于A的摩擦力不止一个 | |
| C. | 物体B对A的压力大小等于桌面对A的摩擦力大小 | |
| D. | 物体B受五个力作用 |
9.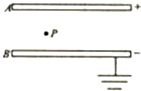 一个平行板电容器充电后与电源断开,负极板B接地,P为两极板间一点,如图所示,用E表示电容器两极板间的电场强度,U表示两极板间的电压,φ表示P点的电势,则下列说法中正确的是( )
一个平行板电容器充电后与电源断开,负极板B接地,P为两极板间一点,如图所示,用E表示电容器两极板间的电场强度,U表示两极板间的电压,φ表示P点的电势,则下列说法中正确的是( )
 一个平行板电容器充电后与电源断开,负极板B接地,P为两极板间一点,如图所示,用E表示电容器两极板间的电场强度,U表示两极板间的电压,φ表示P点的电势,则下列说法中正确的是( )
一个平行板电容器充电后与电源断开,负极板B接地,P为两极板间一点,如图所示,用E表示电容器两极板间的电场强度,U表示两极板间的电压,φ表示P点的电势,则下列说法中正确的是( )| A. | 若保持B极板不动,将极板A向下移动少许,则U变小,E不变 | |
| B. | 若将一玻璃板插入A、B两极板之间,则C变大,E变大 | |
| C. | 若将A极板向左平行移动少许,则U变小,φ不变 | |
| D. | 若保持A极板不动,将极板B向上移动少许,则U变小,φ不变 |
16.若一个物体的动量发生了变化,则物体运动的(质量不变)( )
| A. | 速度大小一定改变了 | B. | 速度方向一定改变了 | ||
| C. | 速度一定变化了 | D. | 加速度可能为零 |
6.山焦中学10月20号举行运动会,高一的某甲同学参加400米跑步,乙同学参加800米.他们跑完全程的时间分别是56秒和120秒,跑道为400m标准跑道.他们平均速度的大小比较( )
| A. | 甲的大于乙的 | B. | 乙的大于甲的 | C. | 大小相等 | D. | 无法确定 |
13.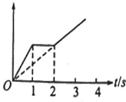 如图所示为某一物体的运动图象,由于画图人粗心未标明是速度-时间图象还是位移-时间图象,但已知物体在第1s内的速度比第3s内的速度大,则下列说法正确的是( )
如图所示为某一物体的运动图象,由于画图人粗心未标明是速度-时间图象还是位移-时间图象,但已知物体在第1s内的速度比第3s内的速度大,则下列说法正确的是( )
 如图所示为某一物体的运动图象,由于画图人粗心未标明是速度-时间图象还是位移-时间图象,但已知物体在第1s内的速度比第3s内的速度大,则下列说法正确的是( )
如图所示为某一物体的运动图象,由于画图人粗心未标明是速度-时间图象还是位移-时间图象,但已知物体在第1s内的速度比第3s内的速度大,则下列说法正确的是( )| A. | 该图一定是v-t图象 | |
| B. | 该图一定是s-t图象 | |
| C. | 物体在第3s内的速度越来越大 | |
| D. | 物体在第3s内的位移比第1s内的位移大 |
10. 如图甲所示,“飞车走壁”的演员骑着摩托车飞驶在光滑的圆台形筒壁上,筒的轴线垂直于水平面,圆台筒固定不动.现将圆台筒简化为如图乙所示,若演员骑着摩托车先后在A、B两处紧贴着内壁分别在图乙中虚线所示的水平面内做匀速圆周运动,则下列说法正确的是( )
如图甲所示,“飞车走壁”的演员骑着摩托车飞驶在光滑的圆台形筒壁上,筒的轴线垂直于水平面,圆台筒固定不动.现将圆台筒简化为如图乙所示,若演员骑着摩托车先后在A、B两处紧贴着内壁分别在图乙中虚线所示的水平面内做匀速圆周运动,则下列说法正确的是( )
 如图甲所示,“飞车走壁”的演员骑着摩托车飞驶在光滑的圆台形筒壁上,筒的轴线垂直于水平面,圆台筒固定不动.现将圆台筒简化为如图乙所示,若演员骑着摩托车先后在A、B两处紧贴着内壁分别在图乙中虚线所示的水平面内做匀速圆周运动,则下列说法正确的是( )
如图甲所示,“飞车走壁”的演员骑着摩托车飞驶在光滑的圆台形筒壁上,筒的轴线垂直于水平面,圆台筒固定不动.现将圆台筒简化为如图乙所示,若演员骑着摩托车先后在A、B两处紧贴着内壁分别在图乙中虚线所示的水平面内做匀速圆周运动,则下列说法正确的是( )| A. | A处的线速度大于B处的线速度 | B. | A处的角速度大于B处的角速度 | ||
| C. | A处对筒的压力大于B处对筒的压力 | D. | A处的向心力大于B处的向心力 |
 氢气球重16N,空气对它的浮力为22N,由于受水平风力的作用,使系氢气球的绳子和地面成60°角,求
氢气球重16N,空气对它的浮力为22N,由于受水平风力的作用,使系氢气球的绳子和地面成60°角,求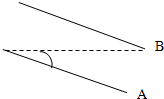 一平行板电容器板长L=4cm,板间距离d=3cm,倾斜放置,使板面与水平方向夹角α=37°,若两板间所加电压U=100V,一带电量q=3×10-10C的负电荷以v0=0.5m/s的速度自A板左边缘水平进入电场,在电场中沿水平方向运动,并从B板右边缘水平飞出,求带电粒子质量为多少?粒子飞出时的速度多大?(Sin37°=0.6,cos37°=0.8)
一平行板电容器板长L=4cm,板间距离d=3cm,倾斜放置,使板面与水平方向夹角α=37°,若两板间所加电压U=100V,一带电量q=3×10-10C的负电荷以v0=0.5m/s的速度自A板左边缘水平进入电场,在电场中沿水平方向运动,并从B板右边缘水平飞出,求带电粒子质量为多少?粒子飞出时的速度多大?(Sin37°=0.6,cos37°=0.8)