��Ŀ����
����Ŀ����ͼ����һˮƽ���ʹ������Ҷ˼�ľ���Ϊ10m��һ�������߹⻬б����h1=4m���ɾ�ֹ�ͷŻ��ϴ��ʹ�����ˣ���֪��=30�㣬�����봫�ʹ���Ķ�Ħ������Ϊ0.1�������ʹ���ֹʱ������ǡ�ܻ����Ҳ�⻬б��h2�߶ȴ����������������ʧ�����ƣ�����������ø�ʽ��ʾ��gȡ10m/s2��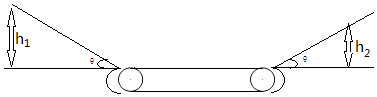
��1���߶�h2Ϊ���٣�
��2�������ʹ���2m/s���ٶ������˶��������һ�ε��ﴫ�ʹ��Ҷ˵�ʱ���Ƕ��٣�
��3�������ʹ���ֹ������������ͣ�ںδ��������˶���·��Ϊ���
���𰸡�
��1���⣺���������̣��ɶ��ܶ����ã�
mg��h1��h2������mgL=0
�ɵ� h2=h1����L=4��0.1��10=3��m��
�𣺸߶�h2Ϊ3m��
��2���⣺�������һ�λ��ϴ��ʹ�ʱ���ٶ�Ϊv0��
�����������б�����»��Ĺ��̣��ɶ��ܶ����ã�
mgh1= ![]()
�ɵ� v0=4 ![]() m/s
m/s
���贫�ʹ�˳ʱ�룬�����ڴ��ʹ��������봫�ʹ�����ʱͨ����λ�ƴ�СΪx�����ɶ��ܶ����ã�
����mgx= ![]() ��
�� ![]()
��� x=38m��L=10m
�������۴��ʹ�˳ʱ�뻹����ʱ�봫�������嶼���ȼ���ֱ���˶�������������Ħ�������䣬���ٶȲ��䣬ʱ����ȣ�����t��
���� L=v0t�� ![]()
�� ��mg=ma
������� ![]()
�����۴��ʹ�˳ʱ�뻹����ʱ�봫�����˶�ʱ�䶼�ǣ� ![]() ��s��
��s��
��3���⣺����б���ǹ⻬�ģ����Ը���������ͣ�ڴ��ʹ��ϣ��������ڴ��ʹ����˶�����·��Ϊs��
���������̣��ɶ��ܶ����ã�
mgh1=��mgs
��� s=40m=4L
�����������ͣ�ڴ��ʹ�����ˣ�
�������һ�λ������б��ʱ�������б���ϻ��е�·��Ϊs1������ڶ��λ����Ҳ�б��ʱ�����Ҳ�б���ϻ��е�·��Ϊs2��
����ڶ��λ������б��ʱ�������б���ϻ��е�·��Ϊs3����������λ����Ҳ�б��ʱ�����Ҳ�б���ϻ��е�·��Ϊs4��
�Ը��ι��̷ֱ���ݶ��ܶ����ã�
mgh2����mgL��mgsin��s1=0
mg��s1��s2��sin�ȩ���mgL=0
mg��s2��s3��sin�ȩ���mgL=0
mg��s3��s2��sin�ȩ���mgL=0
�����˶���·��Ϊ s��= ![]() +s+
+s+ ![]() +2s1+2s2+2s3+s4��
+2s1+2s2+2s3+s4��
������� s��=72m
�������˶���·��Ϊ72m�����ͣ�ڴ��ʹ�����ˣ�
����������1�����ö��ܶ����ԣ�����������ʽ����ø߶�h2��
��2���ȸ��ݶ��ܶ�����������һ�λ��ϴ��ʹ�ʱ���ٶȣ��ٸ���������ٶ��봫�ʹ��ٶȵĹ�ϵ����������˶�������������ţ�ٵڶ����ɺ��˶�ѧ��ʽ���˶�ʱ�䣮
��3������б���ǹ⻬�ģ����Ը���������ͣ�ڴ��ʹ��ϣ��������������ö��ܶ�����������ڴ��ʹ����˶�����·�̣��ٷ�����������ֹͣ��λ�ã�