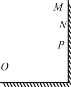��Ŀ����
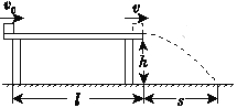
����Ŀ����ͼ����ʾ���ڹ⻬��Եˮƽ�����ڽ���xoy����ϵ���ڵڢ���������ƽ�����������ǿ�糡����ǿ������x�Ḻ����ļнǦ�=45�����ڵڢ�����ֱ��������������ƽ�е�ƽ��C1��C2��������Ϊd1=0��6m���������ֱ���ϵ���ǿ�ų��������Ҷ���y���ϣ���C1��x���غϣ�������˽���������һС��M��С��M������ԭ��O�ľ���ΪL=0��72m���ڵڢ�����ֱ��x�����һ��ƽ��y������y�Ḻ���㹻������ֱƽ��C3��ƽ��C3��x���ϴ���ΪQ������Q��ԭ��O���d2=0��18m���ֽ�һ�������С��������ϵ�P���Գ��ٶ�v0=4![]() m/s��ֱ�ڵ糡����������պô�ֱ��x�ᴩ��C1���ϵ�M�ף�����ų���������֪С�����Ϊ�ʵ㣬С��ıȺ�
m/s��ֱ�ڵ糡����������պô�ֱ��x�ᴩ��C1���ϵ�M�ף�����ų���������֪С�����Ϊ�ʵ㣬С��ıȺ�![]() =20C/kg��P����С��M�ڴ�ֱ�ڵ糡�����ϵľ���Ϊs=
=20C/kg��P����С��M�ڴ�ֱ�ڵ糡�����ϵľ���Ϊs=![]() m�������ǿ�����������
m�������ǿ�����������
��1����ǿ�糡�ij�ǿ��С��
��2��Ҫʹ����С������ײ�ش����ų�����ƽ��C3�ϣ���Ÿ�Ӧǿ�ȵ�ȡֵ��Χ��
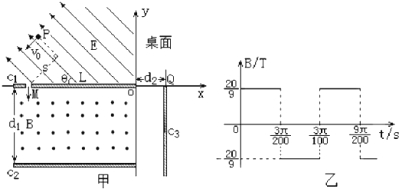
��3����t=0ʱ��С���M�����ų����ų��ĴŸ�Ӧǿ������ͼ��ʱ��������Ա仯��ȡ��ֱֱ������Ϊ�ų�������������С���M�㵽����ƽ��C3�����õ�ʱ������������������λС����
���𰸡���1��![]() N/C����2��
N/C����2��![]() T��B��1T����3��0��15s��
T��B��1T����3��0��15s��
��������
�����������1��С���ڵڢ�����������ƽ���˶��У�
v0t=s
at=v0tan��
��ţ�ٵڶ������У�qE=ma
����ݽ�ã�E=![]() N/C��
N/C��
��2����С��ͨ��M��ʱ���ٶ�Ϊv��
����ƽ���˶����ɣ�v=![]() =8m/s����
=8m/s����
С��ֱ�ų�������������������Բ���˶����켣��ͼ��
��ţ�ٵڶ������У�![]() ��
��
�ã�B=![]()
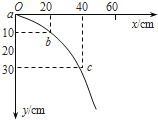
С��պ��ܴ�Q��ʱ�Ÿ�Ӧǿ����ǿ��ΪB1����ʱС��Ĺ켣�뾶ΪR1

��ͼ��ʾ���ɼ��ι�ϵ�У�![]()
�������ݽ�ã�B1=1T��
С��պò���C2������ʱ�Ÿ�Ӧǿ����С��ΪB2����ʱ���ӵĹ켣�뾶ΪR2
�ɼ��ι�ϵ�У�R2=d1��
�������ݽ�ã�B2=![]() T��
T��
�ۺϵôŸ�Ӧǿ�ȵ�ȡֵ��Χ��![]() T��B��1T��
T��B��1T��
��3��С�����ų�������Բ���˶�����뾶ΪR3������ΪT�������ڹ�ʽ�ɵã�
R3=![]()
�����R3=0��18m
T=![]()
�����T=![]() s
s
�ɴų�����T0=![]() ����֪С���ڴų����˶��Ĺ켣��ͼ��һ���ų�������С����x�᷽���λ��Ϊ3r=0��54m
����֪С���ڴų����˶��Ĺ켣��ͼ��һ���ų�������С����x�᷽���λ��Ϊ3r=0��54m
L��3r=0��18m

����С��պô�ֱy�᷽���뿪�ų�
���ڴų����˶���ʱ��t1=![]() +
+![]() +
+![]() =
=![]() =0��13s
=0��13s
�뿪�ų�������ƽ��C3�����õ�ʱ��t2=![]() =0��02s
=0��02s
С���M�㵽����ƽ��C3��������ʱ��t=t1+t2=0��02+0��13=0��15s��