��Ŀ����
 ��ͼ��ʾ����ֱƽ�����з�Χ�㹻��ˮƽ�������ǿ�糡�������ߵ�����д�ֱֽ���������ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB��һ��Ե?�ιܸ�������ֱ�˺�һ�뾶ΪR�İ�Բ����ɣ��̶���ֽ�����ڵ���ֱƽ���ڣ�PQ��MNˮƽ���㹻������Բ��MAP�ڴų��߽���࣬P��M���ڴų������ϣ�NMAP���ǹ⻬�ģ�����һ����Ϊm��������Ϊ+q��С������MN�ˣ������ܵ��ĵ糡��Ϊ������
��ͼ��ʾ����ֱƽ�����з�Χ�㹻��ˮƽ�������ǿ�糡�������ߵ�����д�ֱֽ���������ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB��һ��Ե?�ιܸ�������ֱ�˺�һ�뾶ΪR�İ�Բ����ɣ��̶���ֽ�����ڵ���ֱƽ���ڣ�PQ��MNˮƽ���㹻������Բ��MAP�ڴų��߽���࣬P��M���ڴų������ϣ�NMAP���ǹ⻬�ģ�����һ����Ϊm��������Ϊ+q��С������MN�ˣ������ܵ��ĵ糡��Ϊ������| 1 | 2 |
��1����DM��ľ���x0��
��2��������������С����һ��ͨ����O�ȸߵ�A��ʱ��˶�С���������Ĵ�С��
��3����С����PQ��Ķ�Ħ������Ϊ�̣������ֹĦ�����뻬��Ħ������С��ȣ����ֽ�С������M���Ҳ�6R���ɾ�ֹ��ʼ�ͷţ���С���������˶������п˷�Ħ���������Ĺ���
��������1����D��PΪ�о����̣����ö��ܶ������DM��ľ��룮
��2����D��AΪ�о����̣����ö��ܶ������A����ٶȣ�����ţ�ٵڶ����ɣ��ذ뾶�����Ϻ����ṩ�������������˶�С���������Ĵ�С��
��3��������Ħ�����Ĵ�С��糡���Ĵ�С��ϵ����Ħ�������ڵ糡�������˶���P���Ҳ�ֹͣ����Ħ����С�ڵ糡������������DP�������˶������ݶ��ܶ������Ħ�������Ĺ���
��2����D��AΪ�о����̣����ö��ܶ������A����ٶȣ�����ţ�ٵڶ����ɣ��ذ뾶�����Ϻ����ṩ�������������˶�С���������Ĵ�С��
��3��������Ħ�����Ĵ�С��糡���Ĵ�С��ϵ����Ħ�������ڵ糡�������˶���P���Ҳ�ֹͣ����Ħ����С�ڵ糡������������DP�������˶������ݶ��ܶ������Ħ�������Ĺ���
����⣺��1���ɶ��ܶ���qEx0-2mgR=0
qE=
mg
��x0=4R
��DM��ľ���Ϊ4R��
��2����С����A���ٶ�vA
�ɶ��ܶ���qE��x0+R��-mgR=
mvA2
vA=
����������ʽ��N-qvAB-qE=m
N=
mg+qB
����˶�С���������Ĵ�СN=
mg+qB
��
��3������mg��qE���̡�
С����P���Ҳ�S1����ֹ
qE��6R-S1��-mg?2R-��mgS1=0
S1=
��W=��mgS1=
����mg��qE���̣�
�������������˶������ֻ����PD֮���˶�����˷�Ħ����ΪW
��qE?6R-mg?2R-W=0
��W=mgR
��С���������˶������п˷�Ħ���������Ĺ�Ϊ
��mgR��
qE=
| 1 |
| 2 |
��x0=4R
��DM��ľ���Ϊ4R��
��2����С����A���ٶ�vA
�ɶ��ܶ���qE��x0+R��-mgR=
| 1 |
| 2 |
vA=
| 3gR |
����������ʽ��N-qvAB-qE=m
| ||
| R |
N=
| 7 |
| 2 |
| 3gR |
����˶�С���������Ĵ�СN=
| 7 |
| 2 |
| 3gR |
��3������mg��qE���̡�
| 1 |
| 2 |
qE��6R-S1��-mg?2R-��mgS1=0
S1=
| 2R |
| 1+2�� |
��W=��mgS1=
| 2��mgR |
| 1+2�� |
����mg��qE���̣�
| 1 |
| 2 |
��qE?6R-mg?2R-W=0
��W=mgR
��С���������˶������п˷�Ħ���������Ĺ�Ϊ
| 2��mgR |
| 1+2�� |
���������ö��ܶ�����������ʵ�ѡȡ�о��Ĺ��̣����ݶ��ܶ����г�����ʽ��⣮

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
 ��2011?������ģ�⣩�ס��ҡ�������С��ֱ�λ����ͼ��ʾ����ֱƽ���ڣ�������ͬһ����ֱ���ϣ��ױ���ͬһ��ˮƽ���ϣ�ˮƽ���P���ڱ������·�����ͬһʱ�̣����ұ���ʼ�˶�������ˮƽ�ٶ�v0��ƽ���˶�������ˮƽ�ٶ�v0��ˮƽ������������ֱ���˶����������������˶���������
��2011?������ģ�⣩�ס��ҡ�������С��ֱ�λ����ͼ��ʾ����ֱƽ���ڣ�������ͬһ����ֱ���ϣ��ױ���ͬһ��ˮƽ���ϣ�ˮƽ���P���ڱ������·�����ͬһʱ�̣����ұ���ʼ�˶�������ˮƽ�ٶ�v0��ƽ���˶�������ˮƽ�ٶ�v0��ˮƽ������������ֱ���˶����������������˶��������� ��ͼ��ʾ����ֱƽ�����з�Χ�㹻��ˮƽ�������ǿ�糡���糡ǿ��ΪE��һ��Ե���������ֱ�˺�һ�뾶R=1.6m���ķ�֮һԲ����MN��ɣ��̶�����ֱ���ڣ���ֱ����Բ���˵����ӵ�ֱ���M��N����ֱ��PM��ˮƽ��NQ���㹻����PMN�ι⻬������һ����Ϊm1=0.2kg���������Ϊ+q��С������PM���ϣ���M����Ϸ���D�㾲ֹ�ͷţ�ǡ���ܴﵽN�㣮��֪q=2��10-2C��E=2��102N/m��gȡ10m/s2��
��ͼ��ʾ����ֱƽ�����з�Χ�㹻��ˮƽ�������ǿ�糡���糡ǿ��ΪE��һ��Ե���������ֱ�˺�һ�뾶R=1.6m���ķ�֮һԲ����MN��ɣ��̶�����ֱ���ڣ���ֱ����Բ���˵����ӵ�ֱ���M��N����ֱ��PM��ˮƽ��NQ���㹻����PMN�ι⻬������һ����Ϊm1=0.2kg���������Ϊ+q��С������PM���ϣ���M����Ϸ���D�㾲ֹ�ͷţ�ǡ���ܴﵽN�㣮��֪q=2��10-2C��E=2��102N/m��gȡ10m/s2�� ��ͼ��ʾ���ס��ҡ�����С��ֱ�λ����ͼ��ʾ����ֱƽ���ڣ��ס�����ͬһ����ֱֱ���ϣ��ס�����ͬһ��ˮƽ���ϣ�P���ڱ������·���ijʱ�̣��ס��ҡ���ͬʱ��ʼ�˶�������ˮƽ�ٶ�v0ƽ�ף�����ˮƽ�ٶ�v0��ˮƽ������������ֱ���˶����������������˶���������˵����ȷ���ǣ�������
��ͼ��ʾ���ס��ҡ�����С��ֱ�λ����ͼ��ʾ����ֱƽ���ڣ��ס�����ͬһ����ֱֱ���ϣ��ס�����ͬһ��ˮƽ���ϣ�P���ڱ������·���ijʱ�̣��ס��ҡ���ͬʱ��ʼ�˶�������ˮƽ�ٶ�v0ƽ�ף�����ˮƽ�ٶ�v0��ˮƽ������������ֱ���˶����������������˶���������˵����ȷ���ǣ������� �ס��ҡ�������С��ֱ�λ����ͼ��ʾ����ֱƽ���ڣ��ס�����ͬһ��ˮƽ���ϡ����Ϊs���ҡ�����ͬһ����ֱ���ϡ����Ϊh��������ͬһʱ�̿�ʼ�˶������Գ��ٶ�v����ƽ���˶������Գ��ٶ�v������ֱ�����˶����������������˶�����v����
�ס��ҡ�������С��ֱ�λ����ͼ��ʾ����ֱƽ���ڣ��ס�����ͬһ��ˮƽ���ϡ����Ϊs���ҡ�����ͬһ����ֱ���ϡ����Ϊh��������ͬһʱ�̿�ʼ�˶������Գ��ٶ�v����ƽ���˶������Գ��ٶ�v������ֱ�����˶����������������˶�����v����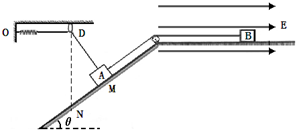 ��2013?�Ĵ�������ͼ��ʾ����ֱƽ���ڣ�����A�ʹ����������B�ÿ�������ֵľ�Ե�������ӣ��ֱ�ֹ����Ǧ�=370�Ĺ⻬б���ϵ�M��ʹֲھ�Եˮƽ���ϣ��������Ӧƽ��ƽ�У�����ϵ��K=5N/m���ᵯ��һ�˹̶���0�㣬һ������һ���������̶��Ĺ⻬С��D��A���������ɴ���ԭ��������ǡ����ֱ��DM��ֱ��б�森ˮƽ�洦�ڳ�ǿE=5��104N/C������ˮƽ���ҵ���ǿ�糡�У���֪A��B�������ֱ�ΪmA=0.1kg��mB=0.2kg��B���������q=+4��l0-6C�������������Ϊ�ʵ㣬���ƻ���������Ħ�����������쳤������ʼ���ڵ������ڣ�B�������䣮ȡg=lOm/s2��sin37��=0.6��cos37��=0.8��
��2013?�Ĵ�������ͼ��ʾ����ֱƽ���ڣ�����A�ʹ����������B�ÿ�������ֵľ�Ե�������ӣ��ֱ�ֹ����Ǧ�=370�Ĺ⻬б���ϵ�M��ʹֲھ�Եˮƽ���ϣ��������Ӧƽ��ƽ�У�����ϵ��K=5N/m���ᵯ��һ�˹̶���0�㣬һ������һ���������̶��Ĺ⻬С��D��A���������ɴ���ԭ��������ǡ����ֱ��DM��ֱ��б�森ˮƽ�洦�ڳ�ǿE=5��104N/C������ˮƽ���ҵ���ǿ�糡�У���֪A��B�������ֱ�ΪmA=0.1kg��mB=0.2kg��B���������q=+4��l0-6C�������������Ϊ�ʵ㣬���ƻ���������Ħ�����������쳤������ʼ���ڵ������ڣ�B�������䣮ȡg=lOm/s2��sin37��=0.6��cos37��=0.8��