题目内容
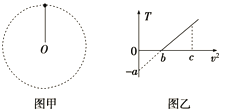
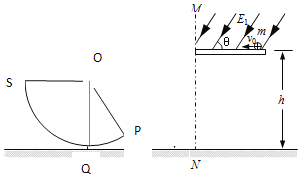
【题目】如图所示,水平地面上方竖直边界MN右侧离地面h=0.65m处有长为L=2m的粗糙水平绝缘平台,动摩擦因素μ=0.68,平台的左边缘与MN重合,平台右边缘A点有一质量m=0.1kg、电量q=0.1C的带正电滑块(可视为质点),以初速度v0=2m/s向左运动,此时平台上方存在E=25N/C的匀强电场,电场方向与水平方向成θ角,大小为37°,方向指向左下方。MN左侧竖立着一个光滑的圆轨道PQS,O为轨道圆心,OP与竖直夹角也为θ角,轨道末端S竖直。若滑块离开平台左侧后恰能沿P点的切线进入圆轨道,因圆轨道非绝缘,滑块运动到圆轨道之后失去了所有的电量。若整个过程滑块均可视为质点g=10m/s2.求
(1)滑块离开绝缘平台时,摩擦力做功的功率大小;
(2)滑块运动到Q点时,对轨道的压力;
(3)滑块最终停留在D点,求AD的距离。
【答案】(1)6.8W(2)3.1N,竖直向下(3)0.72m
【解析】
(1)取向左为正方向,滑块在粗糙水平绝缘平台运动时加速度为a1,根据受力分析水平方向有:ma1=Fqcosθ-μN
竖直方向有:N=mg+Fqsinθ
根据摩擦力公式有:f1=μN
根据电场力公式有:Fq=qE
滑块作匀加速直线运动,根据运动学公式有:![]()
摩擦力做功的功率大小为:![]()
联立上式,解得:vt=4m/s,![]()
(2)滑块出平台后作初速度为vt的平抛运动至P点,设其竖直位移为h1,圆形轨道的半径为R
则根据题意可以得到数学关系:Rcosθ+h-h1=R
滑块在P点水平方向速度仍为vt,设其竖直方向速度为vy,由于滑块至P点沿切线进入轨道,则有:![]()
又:![]()
设滑块运动到Q点速度为vQ滑块出平台后运动到点Q的过程机械能守恒,则:
![]()
滑块在Q点由重力及轨道的支持力NQ提供向心力,则:![]()
联立上式解得:NQ=3.1N
由牛顿第三定律可知,滑块运动到Q点时,对轨道的压力为3.1N,方向竖直向下。
(3)滑块在圆弧轨道运动结束后又回抛至平台最左端,并且此刻其竖直方向速度刚好为零,水平方向速度大小与vt一致,随后在摩擦力下作匀减速运动,运动位移为S2后停下,则有:AD+s2=L
根据动能定理有:![]()
联立上式,解得:AD≈0.72m