题目内容
7. 一质量为m的小球系于长度分别为L1、L2的两根细线上,L2的一端悬挂在天花板上.与竖直方向夹角为θ=60°,L2水平拉直.小球处于平衡状态.若剪断细线L2,以下说法正确的是( )
一质量为m的小球系于长度分别为L1、L2的两根细线上,L2的一端悬挂在天花板上.与竖直方向夹角为θ=60°,L2水平拉直.小球处于平衡状态.若剪断细线L2,以下说法正确的是( )| A. | 剪断细线瞬间细绳L1上的拉力为$\sqrt{3}$mg | |
| B. | 小球摆到最低点时细线L1上的拉力为3mg | |
| C. | 小球摆到最低点时的速度为$\sqrt{2g{L}_{1}}$ | |
| D. | 小球摆到最低点时的角速度为$\sqrt{\frac{g}{{L}_{1}}}$ |
分析 剪断细线瞬间,小球速度为零,则沿着绳子方向的合力为零,根据平衡条件求解L1上的拉力,小球运动到最低点的过程中,根据动能定理求出到达最低点的速度,在最低点,根据向心力公式求解绳子的拉力,根据$ω=\frac{v}{r}$求解角速度.
解答 解:A、剪断细线瞬间,小球速度为零,则沿着绳子方向的合力为零,则有L1上的拉力F=mgcos60°=$\frac{1}{2}mg$,故A错误;
B、小球运动到最低点的过程中,根据动能定理得:$\frac{1}{2}m{v}^{2}=mg({L}_{1}-{L}_{1}cos60°)$=$\frac{1}{2}mg{L}_{1}$,
解得:v=$\sqrt{g{L}_{1}}$
在最低点,根据向心力公式得:
${F}_{1}-mg=m\frac{{v}^{2}}{{L}_{1}}$
解得:F1=2mg,故BC错误;
D、小球摆到最低点时的角速度$ω=\frac{v}{{L}_{1}}=\sqrt{\frac{g}{{L}_{1}}}$,故D正确.
故选:D
点评 本题考查了共点力平衡、牛顿第二定律、动能定理的基本运用.注意剪断l2线,绳子的拉力发生突变,该瞬间沿绳子方向的合力为零,合力沿垂直绳子方向.

练习册系列答案
相关题目
17.下列有关自由落体运动的说法中正确的是( )
| A. | 伽利略对物体下落规律的探究方法对后来的科学研究有重大的启蒙作用 | |
| B. | 满足速度跟时间成正比的运动一定是自由落体运动 | |
| C. | 做自由落体运动的物体,加速度都是相等的 | |
| D. | 在南极质量大的石头比质量小的石头下落更快 |
18.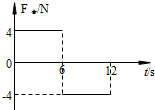 放置在水平面上的物体质量为m=2.0kg,受到沿水平方向的恒定拉力作用,拉力对物体作用了6.0s后撤去,物体在整个运动过程中受到的外力的合力F合的变化情况如图所示.则根据题中所给条件和图象可以求出的物理量有( )
放置在水平面上的物体质量为m=2.0kg,受到沿水平方向的恒定拉力作用,拉力对物体作用了6.0s后撤去,物体在整个运动过程中受到的外力的合力F合的变化情况如图所示.则根据题中所给条件和图象可以求出的物理量有( )
①物体和水平面间的动摩擦因数 ②物体运动的最大速度
③物体整个运动的位移 ④物体前6秒内的位移.
 放置在水平面上的物体质量为m=2.0kg,受到沿水平方向的恒定拉力作用,拉力对物体作用了6.0s后撤去,物体在整个运动过程中受到的外力的合力F合的变化情况如图所示.则根据题中所给条件和图象可以求出的物理量有( )
放置在水平面上的物体质量为m=2.0kg,受到沿水平方向的恒定拉力作用,拉力对物体作用了6.0s后撤去,物体在整个运动过程中受到的外力的合力F合的变化情况如图所示.则根据题中所给条件和图象可以求出的物理量有( )①物体和水平面间的动摩擦因数 ②物体运动的最大速度
③物体整个运动的位移 ④物体前6秒内的位移.
| A. | ①② | B. | ①③ | C. | ①②③ | D. | ①②③④ |
19.在某一高度以v0=50m/s的初速度竖直上抛一个小球(不计空气阻力),当小球速度大小为10m/s时,以下判断正确的是(g取10m/s2)( )
| A. | 小球在这段时间的平均速度大小可能为30m/s,方向向上 | |
| B. | 小球在这段过程的运动时间为6秒,平均速度方向向下 | |
| C. | 小球在这段的路程可能为120m或130m | |
| D. | 小球的位移大小一定是120m |
16.已知地球质量为M,半径为R,自转周期为T,地球同步卫星质量为m,引力常量为G,有关同步卫星,下列表述正确的是( )
| A. | 卫星运行时受到的向心力大小为G$\frac{Mm}{{R}^{2}}$ | |
| B. | 卫星的运行速度小于第一宇宙速度 | |
| C. | 卫星运行的向心加速度小于地球表面的重力加速度 | |
| D. | 卫星距地面的高度为$\root{3}{\frac{GM{T}^{2}}{4{π}^{2}}}$ |
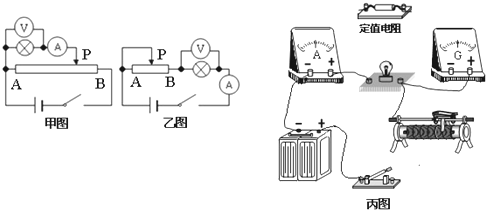
 如图所示,一水平传送带以v0=3.0m/s顺时针传送,水平部分长L=3.0m,其右端与一倾斜角θ=37°的斜面平滑相连,斜面长0.5m,一个物块(可视为质点)无初速度地放在传送带最左端,已知物块与传送带间的动摩擦因数μ1=0.3,与斜面间的动摩擦因数为μ2=0.5,物块由传送带右端滑上斜面过程中无能量损失(g=10m/s2,sin 37°=0.6),求:物块能否到达斜面顶端?若能说明理由,若不能则求出物块上升的最大高度.
如图所示,一水平传送带以v0=3.0m/s顺时针传送,水平部分长L=3.0m,其右端与一倾斜角θ=37°的斜面平滑相连,斜面长0.5m,一个物块(可视为质点)无初速度地放在传送带最左端,已知物块与传送带间的动摩擦因数μ1=0.3,与斜面间的动摩擦因数为μ2=0.5,物块由传送带右端滑上斜面过程中无能量损失(g=10m/s2,sin 37°=0.6),求:物块能否到达斜面顶端?若能说明理由,若不能则求出物块上升的最大高度.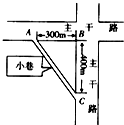 如图所示为某城市两条垂直相交的主干路的平面图,其中A、C两处各有一个公交站,AB=300m、BC=400cm,AC之间有一条小巷,某同学刚到A车站时,公交车恰好由静止启动,于是该同学立刻沿AC小巷奔跑,想赶上将在C处进站的该公交车.已知公交车在30s时间内能匀加速到14m/s,并以该速率行驶,进站时匀减速;且匀加速、匀减速的加速度大小相等,该同学奔跑中,匀减速过程加速度的大小是匀加速过程加速度大小的3倍,求该同学匀加速过程的加速度至少多大,才能在C点赶上该公交车?
如图所示为某城市两条垂直相交的主干路的平面图,其中A、C两处各有一个公交站,AB=300m、BC=400cm,AC之间有一条小巷,某同学刚到A车站时,公交车恰好由静止启动,于是该同学立刻沿AC小巷奔跑,想赶上将在C处进站的该公交车.已知公交车在30s时间内能匀加速到14m/s,并以该速率行驶,进站时匀减速;且匀加速、匀减速的加速度大小相等,该同学奔跑中,匀减速过程加速度的大小是匀加速过程加速度大小的3倍,求该同学匀加速过程的加速度至少多大,才能在C点赶上该公交车?