题目内容
（1）开普勒第三定律告诉我们：行星绕太阳一周所需时间的平方跟椭圆轨道半长径的立方之比是一个常量．如果我们将行星绕太阳的运动简化为匀速圆周运动，请你运用牛顿第二定律、万有引力定律及圆周运动公式，推出这一规律
（2）太阳系只是银河系中一个非常渺小的角落，银河系中至少还有3000多亿颗恒星，银河系中心的质量相当于400万颗太阳的质量．通过观察发现，恒星绕银河系中心运动的规律与开普勒第三定律存在明显的差异，且周期的平方跟圆轨道半径的立方之比随半径的增大而减小．请你对上述现象发表看法．
（2）太阳系只是银河系中一个非常渺小的角落，银河系中至少还有3000多亿颗恒星，银河系中心的质量相当于400万颗太阳的质量．通过观察发现，恒星绕银河系中心运动的规律与开普勒第三定律存在明显的差异，且周期的平方跟圆轨道半径的立方之比随半径的增大而减小．请你对上述现象发表看法．
分析：1、行星绕太阳做匀速圆周运动，根据万有引力提供向心力G
=mr(
)2，化简可推导出
=
，行星绕太阳一周所需时间的平方跟椭圆轨道半长径的立方之比只与中心天体--太阳的质量有关．
2、根据
=
，比值减小的原因，只有一个那就是中心天体的质量变大．
| Mm |
| r2 |
| 2π |
| T |
| T2 |
| r3 |
| 4π2 |
| GM |
2、根据
| T2 |
| r3 |
| 4π2 |
| GM |
解答：解：（1）行星绕太阳做匀速圆周运动，所需要的向心力由万有引力提供，G
=mr(
)2
化简得
=
．
即：行星绕太阳一周所需时间的平方跟椭圆轨道半长径的立方之比是一个常量．
（2）由关系式
=
可知：周期的平方跟圆轨道半径的立方之比的大小与圆心处的等效质量有关，因此半径越大，等效质量越大．
观点一：银河系中心的等效质量，应把圆形轨道以内的所有恒星的质量均计算在内，因此半径越大，等效质量越大．
观点二：银河系中心的等效质量，应该把圆形轨道以内的所有质量均计算在内，在圆轨道以内，可能存在一些看不见的、质量很大的暗物质，因此半径越大，等效质量越大．
| Mm |
| r2 |
| 2π |
| T |
化简得
| T2 |
| r3 |
| 4π2 |
| GM |
即：行星绕太阳一周所需时间的平方跟椭圆轨道半长径的立方之比是一个常量．
（2）由关系式
| T2 |
| r3 |
| 4π2 |
| GM |
观点一：银河系中心的等效质量，应把圆形轨道以内的所有恒星的质量均计算在内，因此半径越大，等效质量越大．
观点二：银河系中心的等效质量，应该把圆形轨道以内的所有质量均计算在内，在圆轨道以内，可能存在一些看不见的、质量很大的暗物质，因此半径越大，等效质量越大．
点评：本题主要考查万有引力提供向心力这个关系，并能根据这个关系推导开普勒第三定律，难度不大，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
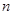次方与其公转周期的平方的比值都相等，期中