题目内容
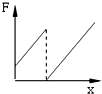
 如图所示,光滑斜面上质量相等的两木块A、B用一轻弹簧相连接,整个系统处于平衡状态,B木块由挡板C挡住.现用一沿斜面向上的拉力F拉动木块A,使木块A沿斜面向上做匀加速直线运动.研究从力F刚作用在A木块的瞬间到木块B刚离开挡板的瞬间这一过程,并且选定该过程中木块A的起点位置为坐标原点,则如图所示图象中能表示力F和木块A的位移x之间关系的是
如图所示,光滑斜面上质量相等的两木块A、B用一轻弹簧相连接,整个系统处于平衡状态,B木块由挡板C挡住.现用一沿斜面向上的拉力F拉动木块A,使木块A沿斜面向上做匀加速直线运动.研究从力F刚作用在A木块的瞬间到木块B刚离开挡板的瞬间这一过程,并且选定该过程中木块A的起点位置为坐标原点,则如图所示图象中能表示力F和木块A的位移x之间关系的是
- A.
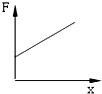
- B.
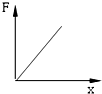
- C.
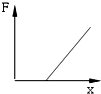
- D.
A
分析:以木块A为研究对象,分析受力情况,根据牛顿第二定律得出F与A位移x的关系式,再选择图象.
解答:设原来系统静止时弹簧的压缩长度为x0,当木块A的位移为x时,弹簧的压缩长度为(x0-x),弹簧的弹力大小为k(x0-x),根据牛顿第二定律得
F+k(x0-x)-mgsinθ=ma
得到,F=kx-kx0+ma+mgsinθ,
又kx0=mgsinθ,
则得到F=kx+ma
可见F与x是线性关系,当x=0时,kx+ma>0.故A正确,B、C、D错误.
故选A.
点评:本题根据牛顿第二定律得到F与x的解析式,再选择图象是常用的思路.
分析:以木块A为研究对象,分析受力情况,根据牛顿第二定律得出F与A位移x的关系式,再选择图象.
解答:设原来系统静止时弹簧的压缩长度为x0,当木块A的位移为x时,弹簧的压缩长度为(x0-x),弹簧的弹力大小为k(x0-x),根据牛顿第二定律得
F+k(x0-x)-mgsinθ=ma
得到,F=kx-kx0+ma+mgsinθ,
又kx0=mgsinθ,
则得到F=kx+ma
可见F与x是线性关系,当x=0时,kx+ma>0.故A正确,B、C、D错误.
故选A.
点评:本题根据牛顿第二定律得到F与x的解析式,再选择图象是常用的思路.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
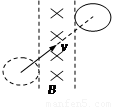
如图所示,光滑水平面上存在有界匀强磁场,直径与磁场宽度相同的金属圆形线框以一定的初速度斜向匀速通过磁场。在必要的时间段内施加必要的水平拉力保证其匀速运动,则
| A.金属框内感应电流方向先顺时针再逆时针 |
| B.金属框内感应电流先增大后减小 |
| C.水平拉力方向与速度同向 |
| D.水平拉力方向与速度方向无关 |
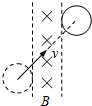 如图所示,光滑水平面上存在有界匀强磁场,直径与磁场宽度相同的金属圆形线框以一定的初速度斜向匀速通过磁场.在必要的时间段内施加必要的水平拉力保证其匀速运动,则
如图所示,光滑水平面上存在有界匀强磁场,直径与磁场宽度相同的金属圆形线框以一定的初速度斜向匀速通过磁场.在必要的时间段内施加必要的水平拉力保证其匀速运动,则