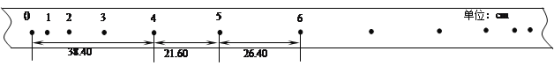题目内容
【题目】一个有一定厚度的圆盘，可以绕通过中心垂直于盘面的水平轴转动．用下面的方法测量它匀速转动时的角速度．
实验器材：电磁打点计时器、米尺、纸带、复写纸片．
实验步骤：
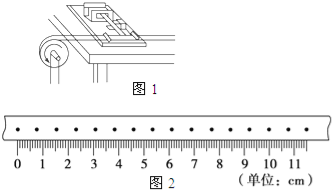
（1）如图1所示，将电磁打点计时器固定在桌面上，将纸带的一端穿过打点计时器的限位孔后，固定在待测圆盘的侧面上，使得圆盘转动时，纸带可以卷在圆盘侧面上．
（2）启动控制装置使圆盘转动，同时接通电源，打点计时器开始打点．
（3）经过一段时间，停止转动和打点，取下纸带，进行测量．
①由已知量和测得量表示的角速度的表达式为ω= ，式中各量的意义是： ．
②某次实验测得圆盘半径r=5.50×10﹣2m，得到的纸带的一段如图2所示，求得角速度为 ．
【答案】①
，式中T为电磁打点计时器打点的周期，r为圆盘的半径，L是用米尺测量的纸带上选定的两点间的长度，n为选定的两点间的打点周期数；
②6.97rad/s
【解析】试题分析：
①在纸带上取两点为n个打点周期，距离为L，则圆盘的线速度为：
，则圆盘的角速度ω=
，式中T为电磁打点计时器打点的周期，r为圆盘的半径，L是用米尺测量的纸带上选定的两点间的长度，n为选定的两点间的打点周期数．
②从图中可知第一个点到最后一个点共有n=15个周期，其总长度L=11.50cm．代入数据解得：ω="6.97" rad/s．
故答案为：①，式中T为电磁打点计时器打点的周期，r为圆盘的半径，L是用米尺测量的纸带上选定的两点间的长度，n为选定的两点间的打点周期数；②6.97rad/s．
练习册系列答案
相关题目
