题目内容
(10分)如图所示，质量为60kg的滑雪运动员，在倾角θ为37°的斜坡顶端，从静止开始自由下滑50m到达坡底，用时5s，然后沿着水平路面继续自由滑行，直至停止，不计拐角处能量损失，滑板与斜面及水平面间的动摩擦因数相同，g取10m/s2，sin37°＝0.6，cos37°＝0.8，求：( )
⑴运动员下滑过程中的加速度大小；
⑵滑板与坡面间的滑动摩擦力大小；
⑶运动员在水平路面上滑行的时间。
⑴a1＝4m/s2；⑵f1＝120N；⑶t2＝8s
解析试题分析：⑴设运动员在斜坡上下滑的加速度为a1，下滑的时间为t1，根据匀变速直线运动位移公式有：s1＝
，解得：a1＝
m/s2＝4m/s2
⑵运动员在斜坡上下滑时受重力mg、斜坡的支持力N1和滑动摩擦力f1作用，根据牛顿第二定律可知，在沿斜坡向下方向上有：mgsinθ－f1＝ma1
解得f1＝mgsinθ－ma1＝360N－60×4N＝120N
⑶在垂直斜坡方向上有：N1－mgcosθ＝0
设滑板与斜面及水平面间的动摩擦因数为μ，根据滑动摩擦定律有：f1＝μN1
根据匀变速直线运动平均速度公式可知，运动员滑至坡底的速度为：v＝
运动员在水平面上滑行时，受重力mg、水平面的支持力N2和滑动摩擦力f2作用，根据牛顿第二定律可知，运动员在水平面上滑行的加速度为：a2＝
＝－μg
根据匀变速直线运动速度公式可知，运动员在是平面上滑行的时间为：t2＝
联立以上各式，并代入数据解得：t2＝8s
练习册系列答案
阅读快车系列答案
相关题目
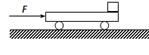
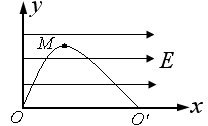
，其上、下两端点A、B间的距离是3.84m．传送带在电动机的带动下，以4.0m/s顺时针匀速运转．现将质量为10kg的工件（可视为质点）轻放于传送带的A点，已知工件与传送带间的动摩擦因数为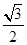
，则在传送带将工件从A点传送到B点过程中，
；求：