��Ŀ����
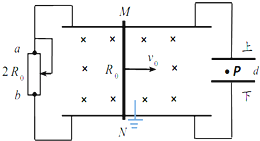
����Ŀ����ͼ��ʾ�������⻬��ƽ�н������촦��ͬһˮƽ���ڣ����l=0.3m����������M��N��R=0.2���ĵ������ӣ�������費�ƣ������Ͽ����һ������r=0.1��������Ϊm=0.1kg�Ľ����ˣ�����װ�ô�����ֱ���µ���ǿ�ų��У��Ÿ�Ӧǿ��ΪB=0.5T���ֶԽ�����ʩ��ˮƽ��ʹ�������ɾ�ֹ��ʼ��0.5m/s2���ٶ��ȼ����˶��������㹻������ �ٴӸ˿�ʼ�˶���2s��ͨ������R�ĵ���ΪC��
�ڴӸ˿�ʼ�˶����2sĩ��������˲ʱ����ΪW��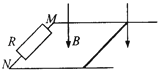
���𰸡�0.5��0.125
����������𣺣�1�����и�Ÿ��߲�����Ӧ�綯�ƣ�E=BLat��������У�![]()
�������� ![]()
��ã�Q=0.5C ��2�����и�Ÿ��߲�����Ӧ�綯�ƣ�E=BLat=0.5��0.3��2��0.5=0.15V��
�ɱպϵ�·ŷķ���ɣ���·������ ![]() ��
��
������ΪF��=BIL=0.5��0.5��0.3N=0.075N
����ţ�ٵڶ�����֪����F=F��+ma=0.075+0.1��0.5=0.125N
�ٶ�v=at=0.5��2=1m/s
��2sĩ��������˲ʱ����ΪP=Fv=0.125��1=0.125W
���Դ��ǣ�0.5��0.125
��������1�����ݵ綯�ƣ�����Q=It �� ������⣮��2����E=BLv�����Ӧ�綯�ƣ�Ȼ����ŷķ���������Ӧ������������ΪF��=BIL������������ţ�ٵڶ�����֪����F=F��+ma �� �����������˲ʱ����ΪP=Fv ��
�����㾫�����������⣬������Ҫ�˽���ζ���(��ζ���������һ������ĸ�Ӧ����������ж��������ֶ���ֻ�����ڵ����и�Ÿ����˶��������������������ֶ����ж�������ζ����ж����)��

 ����˼ά�żӿ���ϵ�д�
����˼ά�żӿ���ϵ�д� �����Ծ�ϵ�д�
�����Ծ�ϵ�д�