题目内容
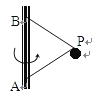
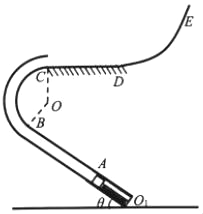
【题目】如图所示是某游戏装置的示意图，ABC为固定在竖直平面内的截面为圆形的光滑轨道，直轨道AB与水平成θ＝37°放置，且与圆弧轨道BC相切连接，AB长为L1＝0.4m，圆弧轨道半径r＝0.25m，C端水平，右端连接粗糙水平面CD和足够长的光滑曲面轨道DE，D是轨道的切点，CD段长为L2＝0.5m。一个质量为m＝1kg的可视为质点的小物块压缩弹簧后被锁定在A点，解除锁定后小物块被弹出，第一次经过D点的速度为vD＝1m/s，小物块每次发射前均被锁定在A位置，通过调整弹簧O1端的位置就可以改变弹簧的弹性势能，已知弹簧的弹性势能最大值为Epm＝13J，小物块与水平面CD间的摩擦因数μ＝0.3．求：
(1)小物块第一次运动到BC轨道的C端时对轨道的压力大小；
(2)小物块第一次发射前弹簧的弹性势能大小：
(3)若小物块被弹出后，最后恰好停在CD中点处，不计小球与弹簧碰撞时的能量损失，则小物块被锁定时的弹性势能可能多大。
【答案】(1)小球运动到C点时对轨道的压力的大小是6N；
(2)解除锁定前弹簧的弹性势能Epo是8.9J；
(3)锁定时弹簧弹性势能Ep的可能值是7.65J，9.15J，10.65J和12.15J。
【解析】
(1)C到D的过程中摩擦力做功，由动能定理可得：
代入数据可得：vc＝2m/s
设小球在C点时轨道对小球的作用力为FN，方向竖直向下。根据牛顿第二定律得：
代入数据解得：FN＝6N
由牛顿第三定律得小球对轨道的压力大小为：FN′＝FN＝6N
(2)A到C的过程中机械能守恒，根据机械能守恒定律，有：
代入数据解得：Epo＝8.9J
(3)要使小球能停在CD的中点，需要在CD段滑过
对整个过程，由能量守恒定律得：
，k＝1，2，3，4…
得：Ep＝6.9+0.75（2k﹣1）（J）
因为弹性势能最大值为：Epm＝13J，所以k取1，2，3，4时，Ep＝7.65J，9.15J，10.65J和12.15J。
