题目内容
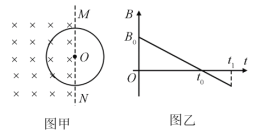
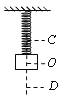
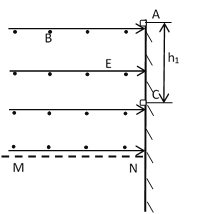
【题目】如图所示，绝缘粗糙的竖直墙壁和水平虚线MN上方之间的区域同时存在正交匀强电场和匀强磁场，电场方向水平向右，大小为E，磁场方向垂直纸面向外，大小为B．现在从A点由静止释放一带正电的可视为质点的带电体，带电体能够沿墙壁下滑，到达C点时刚好离开墙壁，带电体质量为m、电荷量为q，A、C两点间距离为
，C点到虚线MN的距离为
，重力加速度为g.
（1）求带电体运动到刚好离开墙壁时速度大小v；
（2）求带电体由静止下滑到刚好离开墙壁过程中克服摩擦力做的功Wf；
（3）如果带电体到达C点时电场突然变为竖直向上且
，电场的变化对磁场的影响忽略不计，则带电体在电磁场区内的运动过程中，距出发点A的最大距离为多少？
【答案】（1）
（2）
（3）
【解析】
(1)由题意知，当洛伦兹力等于电场力qE时带电体离开MN开始做曲线运动，即：
解得：
(2)从A到C根据动能定理得：
解得：
(3)电场突然变为竖直向上时，由题可知：
带电体在复合场中做匀速圆周运动， 由牛顿第二定律可得：
解得：
由题可知，
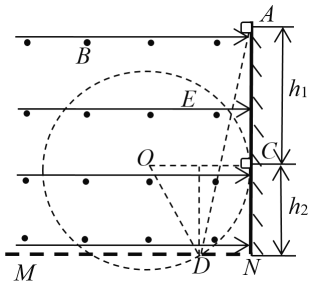
则带电体轨迹与地面相交于D点，
如图所示：
此时距A点的距离最大为：
练习册系列答案
相关题目
