题目内容
19.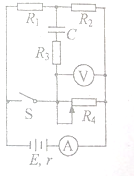 如图所示,电源电动势E=6V,内阻r=1.0Ω,电阻R1=3.0Ω,R2=2.0Ω,R3=9.0Ω,滑动变阻器R4的最大阻值为R4=7.5Ω,电容器的电容C=4.0μF,电压表和电流表均为理想电表,开始时电键S断开,滑动变阻器的滑片处在R4的最左端
如图所示,电源电动势E=6V,内阻r=1.0Ω,电阻R1=3.0Ω,R2=2.0Ω,R3=9.0Ω,滑动变阻器R4的最大阻值为R4=7.5Ω,电容器的电容C=4.0μF,电压表和电流表均为理想电表,开始时电键S断开,滑动变阻器的滑片处在R4的最左端(1)求电键S断开状态下,电容器极板带电量
(2)将电键S闭合,求达到稳定状态过程中,通过电阻R3的电荷量
(3)S闭合的状态下,调节滑动变阻器R4的滑片,由最左端滑至中点,电压表读数的变化量记为△U,电流表读数的变化量记为△I,求$\frac{△U}{△I}$的比值.
分析 (1)当电键断开时,根据闭合电路欧姆定律求出R2两端的电压,结合Q=CU求出电容器极板带电量.
(2)根据闭合电路欧姆定律求出电键闭合时R1两端的电压,结合Q=CU求出电荷量,从而得出通过电阻R3的电荷量.
(3)根据闭合电路欧姆定律得出电压的变化量和电流的变化量,从而得出$\frac{△U}{△I}$的比值.
解答 解:(1)电键S断开时,R1、R2串联,
R2两端的电压${U}_{2}=\frac{E}{{R}_{1}+{R}_{2}+r}{R}_{2}=\frac{6}{1+2+1}×2v=3V$,
则电容器极板的电荷量Q=$C{U}_{2}=4×1{0}^{-6}×3C=1.2×1{0}^{-5}C$.下端带正电.
(2)电键S闭合,R1、R2串联,再与 R4并联,电容器与R1并联,
则总电流I=$\frac{E}{{R}_{并}+r}=\frac{6}{3+1}A=1.5A$,
R1两端的电压${U}_{1}=\frac{7.5}{5+7.5}×3V=1.8V$,
则电容器极板所带的电荷量$Q′=C{U}_{1}=4×1{0}^{-6}×1.8C=7.2×1{0}^{-6}$C,上端带正电,
所以通过电阻R3的电荷量△Q=Q+Q′=1.2×10-5+7.2×10-6=7.32×10-6C.
(3)S闭合时,滑片在最左端时,电压表的读数U=E-Ir=6-1.5×1V=4.5V,
滑至中点时,滑动变阻器阻值为3.75Ω,
则总电流$I′=\frac{E}{{R}_{并}′+r}=\frac{6}{\frac{15}{7}+1}A≈2A$,
则电压表的读数U′=E-I′r=6-2×1V=4V,
可知$\frac{△U}{△I}$=$\frac{4.5-4}{2-1.5}Ω=1Ω$.
答:(1)电键S断开状态下,电容器极板带电量为1.2×10-5C;
(2)通过电阻R3的电荷量为7.32×10-6C.
(3)$\frac{△U}{△I}$的比值为1Ω
点评 本题考查了闭合电路欧姆定律和含容电路的综合,理清串并联电路是解决本题的关键,求解电荷量的变化时,注意极板电量的正负.

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案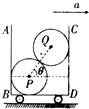 如图所示,在水平地面上内壁光滑的车厢中,两正对竖直面AB、CD间放有光滑均质圆球P、Q,质量分别为mP=5kg、mQ=10kg.当车向右做加速度为a=7.5m/s2的匀加速直线运动时,球P、Q与车厢保持相对静止,两球心连线与水平方向的夹角为θ=53°,重力加速度g=10m/s2.下列说法正确的是( )
如图所示,在水平地面上内壁光滑的车厢中,两正对竖直面AB、CD间放有光滑均质圆球P、Q,质量分别为mP=5kg、mQ=10kg.当车向右做加速度为a=7.5m/s2的匀加速直线运动时,球P、Q与车厢保持相对静止,两球心连线与水平方向的夹角为θ=53°,重力加速度g=10m/s2.下列说法正确的是( )| A. | 球Q受到3个力的作用 | |
| B. | 球P受到球Q的压力是由于球P发生形变而产生的 | |
| C. | 车厢底部受到的压力为50N | |
| D. | 车厢AB面受到的压力为112.5N |
| A. | 12N,16N,20N | B. | 16N,12N,25N | C. | 18N,14N,20N | D. | 16N,12N,20N |
| A. | 电磁波是一种物质,可以在真空中传播 | |
| B. | 磁场中两条磁感线一定不相交,但可以相切 | |
| C. | 首先发现通电导线周围存在磁场的物理学家是特斯拉 | |
| D. | 当一段导线在磁场中运动时,则导线中不一定有感应电流,但一定有感应电动势 |

| A. | 整个运动过程中,质点在C点的状态所对应的位置离出发点最远 | |
| B. | 整个运动过程中,BC段的加速度最大 | |
| C. | 整个运动过程中,CE段的加速度最大 | |
| D. | OA段所表示的运动通过的路程是25m |
| A. | 加速度方向和速度方向一定相同 | |
| B. | 加速度方向和合力方向一定相同 | |
| C. | 加速度在减小而速度在增大的运动不可能存在 | |
| D. | 由F=ma得m=$\frac{F}{a}$,说明物体的质量和F成正比,与a成反比 |
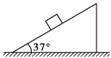 如图所示,在倾角为37°的固定斜面上静置一个质量为5kg的物体,物体与斜面间的动摩擦因数为0.8,若用原长为10cm,劲度系数为2×103N/m的弹簧沿斜面拉物体,使之沿斜面匀速运动,则弹簧的最终长度是多少?(取g=10m/s2)
如图所示,在倾角为37°的固定斜面上静置一个质量为5kg的物体,物体与斜面间的动摩擦因数为0.8,若用原长为10cm,劲度系数为2×103N/m的弹簧沿斜面拉物体,使之沿斜面匀速运动,则弹簧的最终长度是多少?(取g=10m/s2) 如图所示,一圆环与外切正方形线圈均由相同的有绝缘皮的导线制成,并各自形成闭合电路,匀强磁场布满整个方形线圈,当磁场均匀变化时,线圈和圆环中的感应电动势之比为4:π;感应电流之比为1:1;若磁场只布满圆环,则感应电动势之比为1:1.
如图所示,一圆环与外切正方形线圈均由相同的有绝缘皮的导线制成,并各自形成闭合电路,匀强磁场布满整个方形线圈,当磁场均匀变化时,线圈和圆环中的感应电动势之比为4:π;感应电流之比为1:1;若磁场只布满圆环,则感应电动势之比为1:1.