题目内容
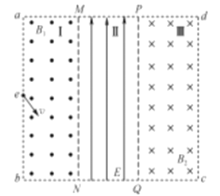
【题目】如图所示,边长为L的正方形abcd区域内,均分成相同的三个矩形区域,区域I内有大小为B1=B、方向垂直纸面向外的匀强磁场,区域II内有方向竖直向上的匀强电场,区域三III内方向垂直纸面向里的匀强磁场.在纸面内有ab边的中点e沿于ab夹角为37°的方向,向磁场I内射入质量为m、电荷量为q的带负电的离子,经磁场偏转后,粒子以MN边夹角从37°的方向进入电场,然后垂直PQ又进入磁场III,粒子经磁场偏转后,恰好从PQ的中点射出磁场III而进入电场区域II.已知sin37°=0.6,cos37°=0.8,不计粒子的重力.求:
(1)粒子从e点射入的速度大小;
(2)匀强电场电场强度的大小E及区域III中匀强磁场磁感应强度B2的大小;
(3)当粒子再次进入区域II时,电场强度大小不变,方向反向,则粒子在abcd边界上出射点的位置离e点的距离及粒子在电场、磁场中运动的总时间.
【答案】(1) ![]() (2)
(2) ![]() ,
,![]() (3)
(3) ![]() ,
, ![]()
【解析】
(1)粒子第一次经过MN的位置为f,由几何关系可知e、f连线与MN垂直.设粒子在区域I中做圆周运动的半径为r1,则r1cos![]() =
=![]()
解得
r1=![]()
设粒子从e点射出的速度大小为v0,根据牛顿第二定律:
qv0B=m![]()
解得
v0=![]()
(2)设粒子第一次经过PQ时速度大小为v1,粒子在电场中的运动是类平拋运动的逆运动,粒子第一次在电场中运动的时间
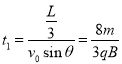
粒子沿场强方向运动的位移:
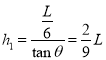
根据运动学公式有:
h1=![]()
根据牛顿第二定律
qE=ma
解得
E=![]()
粒子从g点进区域III时速度大小:
v1=v0sin![]() =
=![]()
在区域III中做圆周运动的半径
r2=![]()
根据牛顿第二定律:
qv1B2 =m![]()
解得区域III中磁场磁感应强度大小
B2=![]()
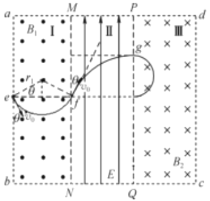
(3)粒子从PQ中点出射后在区域II、I中的运动是粒子从e到g过程的逆运动,如图所示,
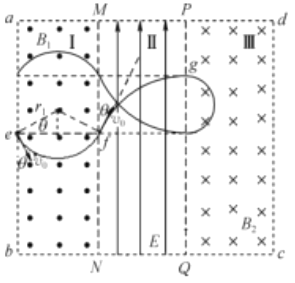
因此粒子从ab边射出磁场时的位置在a、e间离e点的距离为![]()
粒子在区域I中运动的时间
![]()
在区域III中运动的时间:
![]()
因此粒子在电场和磁场中运动的总时间为:
t=t0+2t1+t2=![]()

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案