题目内容
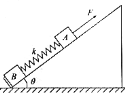
【题目】如图所示，在倾角
光滑斜面上质量均为
的A、B两物体用
的轻弹簧相连，初始时A、B两物体静止放在斜面底端的挡板上。现施加一个沿斜面向上的外力F作用在物体A上，使之能匀加速上升，经
物体B刚要脱离挡板。已知
，
，则下列说法正确的是（ ）
A.所施外力F随时间均匀增大B.物体A运动的加速度为
C.
内外力F所做的功为
D.物体B脱离挡板时物体A的速度为
【答案】C
【解析】
A.弹簧先处于压缩状态，后处于拉伸状态。弹簧处于压缩状态时，对A，根据牛顿第二定律得
F+k△x-mgsinθ=ma
得
F=mgsinθ+ma-k△x，
随着△x的减小，F增大；
弹簧处于拉伸状态时，对A，根据牛顿第二定律得
F-k△x-mgsinθ=ma
得
F=mgsinθ+ma+k△x
随着△x的增大，F增大。根据数学知识知所施外力F随弹簧形变量△x均匀增大，由于A做匀加速运动，当弹簧处于压缩状态时
△x=x1-x
可得：
x1是初始时弹簧的压缩量，可知，△x随时间t不是均匀变化，所以外力F随时间不是均匀增大，同理，当弹簧处于拉伸状态时，外力F随时间不是均匀增大，故A错误.
B. 开始时A、B处于静止状态，对A：
kx1=mgsinθ
解得：
x1=0.15m
B刚要离开挡板时，挡板对B的支持为0，对B：
kx2=mgsinθ
解得：
x2=0.15m
所以从开始到B刚离开挡板时A移动的位移
x=x1+x2=0.3m
由
得
a=3.75m/s2
故B错误.
CD. 物体B脱离挡板时物体A的速度为
v=at=1.5m/s
由于x1=x2，所以初末位置时弹簧的弹性势能相等。对A，根据动能定理得
可得外力F所做的功为
W=14.625J
故C正确，D错误.
【题目】为探究人在运动过程中脚底在接触地面瞬间受到的冲击力问题，实验小组的同学利用落锤冲击地面的方式进行实验，即通过一定质量的重物从某一高度自由下落冲击地面来模拟人体落地时的情况。重物与地面的形变很小，可忽略不计，g 取10m/s2.下表为一次实验过程中的相关数据。根据实验数据可知
重物（包括传感器）的质量 m/kg | 8.5 |
重物下落高度 H/cm | 45 |
重物反弹高度 h/cm | 20 |
最大冲击力 Fm/N | 850 |
重物与地面接触时间 t/s | 0.1 |
A. 重物受到地面的最大冲击力时的加速度大小为100m/s2
B. 重物与地面接触前瞬时的速度大小为2m/s
C. 重物离开地面瞬时的速度大小为3m/s
D. 在重物与地面接触的过程中，重物受到的地面施加的平均作用力是重物所受重力的6 倍
