题目内容
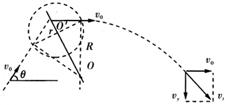
(12分)如图所示,一带电粒子以某一速度在竖直平面内做直线运动,经过一段时间后进入一垂直于纸面向里、磁感应强度为B的圆形匀强磁场区域(图中未画出磁场区域),粒子飞出磁场后垂直电场方向进入宽为L的匀强电场. 电场强度大小为E,方向竖直向上. 当粒子穿出电场时速度大小变为原来的![]() 倍. 已知带电粒子的质量为m,电量为q,重力不计. 粒子进入磁场前的速度与水平方向成60°角,如图.
倍. 已知带电粒子的质量为m,电量为q,重力不计. 粒子进入磁场前的速度与水平方向成60°角,如图. ![]() 试解答:
试解答:
(1)粒子带什么电?
(2)带电粒子在磁场中运动时速度多大?
(3)该圆形磁场区域的最小面积为多大?

【解析】(1)根据粒子在磁场中偏转的情况和左手定则可知,粒子带负电.(2分)
(2)由于洛伦兹力对粒子不做功,故粒子以原来的速率进入电场中,设带电粒子进入电场的初速度为v0,在电场中偏转时做类平抛运动,由题意知粒子离开电场时的末速度大小为![]() ,将vt分解为平行于电场方向和垂直于电场方向的两个分速度:由几何关系知
,将vt分解为平行于电场方向和垂直于电场方向的两个分速度:由几何关系知
![]() ①
① ![]()
![]() ②
②
![]() ③
③ ![]() ④ F=Eq ⑤
④ F=Eq ⑤
联立①②③④⑤求解得:![]() (5分)
(5分)
(3)如图所示,带电粒子在磁场中所受洛伦兹力作为向心力,设在磁场中做圆周运动的半径为R,圆形磁场区域的半径为r,则:
![]() ⑦
⑦
![]() ⑧
⑧
由几何知识可得:r=Rsin30° ⑨
磁场区域的最小面积为S=πr2 ⑩
联立⑧⑨⑩求解得S=![]() (5分)
(5分)

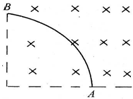 如图所示,一带电粒子垂直射入一自左向右逐渐增强的磁场中,由于周围气体的阻尼作用,其运动径迹的为一段圆弧线,则从图中可以判断(不计重力)( )
如图所示,一带电粒子垂直射入一自左向右逐渐增强的磁场中,由于周围气体的阻尼作用,其运动径迹的为一段圆弧线,则从图中可以判断(不计重力)( )| A、粒子从A点射入,速率逐渐减小 | B、粒子从A点射入,速率逐渐增大 | C、粒子带负电,从B点射入磁场 | D、粒子带正电,从A点射入磁场 |
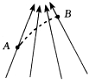 如图所示,一带电粒子只受电场力从A飞到B,径迹如图中虚线所示,下列说法正确的是( )
如图所示,一带电粒子只受电场力从A飞到B,径迹如图中虚线所示,下列说法正确的是( )| A、粒子带正电 | B、粒子加速度不断变小 | C、粒子在A点时动能较大 | D、B点场强小于A点场强 |
 如图所示,一带电粒子在两个固定的等量正点电荷的电场中运动,图中的实线为等势面,虚线ABC为粒子的运动轨迹,其中B点是两点电荷连线的中点,A、C位于同一等势面上.下列说法正确的是( )
如图所示,一带电粒子在两个固定的等量正点电荷的电场中运动,图中的实线为等势面,虚线ABC为粒子的运动轨迹,其中B点是两点电荷连线的中点,A、C位于同一等势面上.下列说法正确的是( ) (2005?长宁区模拟)如图所示,一带电粒子以速度v0沿上板边缘垂直于电场线射入匀强电场,它刚好贴着下板边缘飞出.已知匀强电场两极板长为l,间距为d,求:
(2005?长宁区模拟)如图所示,一带电粒子以速度v0沿上板边缘垂直于电场线射入匀强电场,它刚好贴着下板边缘飞出.已知匀强电场两极板长为l,间距为d,求: 如图所示,一带电粒子以某速度进入水平向右的匀强电场中,在电场力作用下形成图中所示的运动轨迹.M和N是轨迹上的两点,其中M点在轨迹的最右点.不计重力,下列表述正确的是( )
如图所示,一带电粒子以某速度进入水平向右的匀强电场中,在电场力作用下形成图中所示的运动轨迹.M和N是轨迹上的两点,其中M点在轨迹的最右点.不计重力,下列表述正确的是( )