题目内容
【题目】如图所示,一光滑杆固定在底座上,构成支架,放置在水平地面上,光滑杆沿竖直方向,一劲度系数为 k的轻弹簧套在光滑杆上,一套在杆上的圆弧从距弹簧上端H处由静止释放,接触弹簧后,将弹簧压缩,弹簧的形变始终在弹性限度内。已知圆环的质量为m,重力加速度为g,不计空气阻力,取竖直向下为正方向,圆弧刚接触弹簧时的位置为坐标原点O,建立x轴。
(1)请画出弹簧弹力F随压缩量x变化的图线;并根据图像确定弹力做功的规律。
(2)求圆环下落过程中的最大动能![]() ;
;
(3)证明在圆环压缩弹簧的过程中机械能是守恒的。

【答案】(1)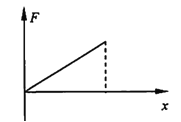 ,
, ![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)根据胡克定律作出F-x图象,图象与x轴围成的面积表示弹力做的功;(2)当圆环所受合力为零时,其最大动能,根据动能定理可求出最大动能;(3)取圆环与弹簧为一个整体,在圆环压缩弹簧的过程中,整体机械能守恒.
(1)由胡可定律可知![]() ,其关系如图所示:
,其关系如图所示:
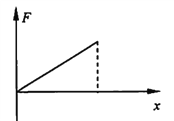
由图中面积可知弹簧弹力做功![]()
(2)在圆环下落过程中,当所受合力为零时,其有最大动能
此时弹簧压缩量为![]() ,
, ![]()
由动能定理可得: ![]()
联立可得: ![]()
(3)圆环接触弹簧后,设在某位置系统动能、重力势能、弹簧弹性势能分别为![]() ,在另一位置系统动能、重力势能、弹簧弹性势能分别为
,在另一位置系统动能、重力势能、弹簧弹性势能分别为![]() 。则
。则
由重力做功与重力势能的关系可知: ![]()
由弹力做功与弹性势能变化的关系可知: ![]()
又由动能定理可得: ![]()
联立可得: ![]()

练习册系列答案
相关题目