题目内容
有一架电梯,启动时匀加速上升,加速度为2m/s2,制动时匀减速上升,加速度为-1m/s2,楼高52m.求:
(1)若上升的最大速度为6m/s,电梯升到楼顶的最短时间是多少?
(2)如果电梯先加速上升,然后匀速上升,最后减速上升,全程共用16秒,上升的最大速度是多少?
解:(1)匀加速直线运动的位移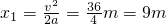 ,匀加速直线运动的时间
,匀加速直线运动的时间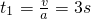 .
.
匀减速直线运动的位移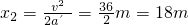 ,匀减速直线运动的时间
,匀减速直线运动的时间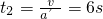 .
.
匀速运动的位移x3=x-x1-x2=25m,则匀速直线运动的时间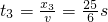 ≈4.2s.
≈4.2s.
则电梯升到楼顶的最短时间为t=t1+t2+t3=13.2s.
(2)设最大速度为v.
则匀加速直线运动的位移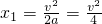 ,匀加速直线运动的时间
,匀加速直线运动的时间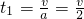 .
.
匀速运动的位移x2=vt2
匀减速直线运动的位移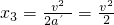 ,匀减速直线运动的时间
,匀减速直线运动的时间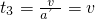 .
.
因为x1+x2+x3=52m,t1+t2+t3=16s
联立解得v=4m/s.
答:(1)若上升的最大速度为6m/s,电梯升到楼顶的最短时间是13.2s.
(2)上升的最大速度是4m/s.
分析:(1)当电梯先匀加速直线运动到最大速度,以最大速度匀速,最后匀减速直线运动到零,这样所需的时间最短.根据运动学公式求出最短的时间.
(2)设最大速度为v,根据匀变速直线运动和匀速直线运动的公式,抓住总位移为52m,总时间为16s,求出上升的最大速度.
点评:解决本题的关键熟练掌握匀变速直线运动的速度位移公式,速度时间公式以及平均速度公式.
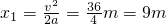 ,匀加速直线运动的时间
,匀加速直线运动的时间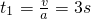 .
.匀减速直线运动的位移
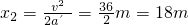 ,匀减速直线运动的时间
,匀减速直线运动的时间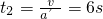 .
.匀速运动的位移x3=x-x1-x2=25m,则匀速直线运动的时间
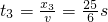 ≈4.2s.
≈4.2s.则电梯升到楼顶的最短时间为t=t1+t2+t3=13.2s.
(2)设最大速度为v.
则匀加速直线运动的位移
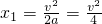 ,匀加速直线运动的时间
,匀加速直线运动的时间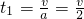 .
.匀速运动的位移x2=vt2
匀减速直线运动的位移
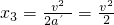 ,匀减速直线运动的时间
,匀减速直线运动的时间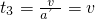 .
.因为x1+x2+x3=52m,t1+t2+t3=16s
联立解得v=4m/s.
答:(1)若上升的最大速度为6m/s,电梯升到楼顶的最短时间是13.2s.
(2)上升的最大速度是4m/s.
分析:(1)当电梯先匀加速直线运动到最大速度,以最大速度匀速,最后匀减速直线运动到零,这样所需的时间最短.根据运动学公式求出最短的时间.
(2)设最大速度为v,根据匀变速直线运动和匀速直线运动的公式,抓住总位移为52m,总时间为16s,求出上升的最大速度.
点评:解决本题的关键熟练掌握匀变速直线运动的速度位移公式,速度时间公式以及平均速度公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目