Question

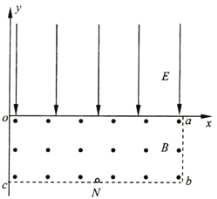
【题目】如图所示，真空中竖直条形区域I存在垂直纸面向外的匀强磁场，条形区域II存在水平向左的匀强电场，磁场和电场宽度均为L且足够长，图中虚线是磁场与电场的分界线，M、N为涂有荧光物质的竖直板，带电粒子打在M、N板上被吸附时就会发出荧光。现有一束带正电粒子从A处以速度v连续不断地射入磁场，入射方向与M板成60°夹角且与纸面平行，已知带正粒子的质量为m，电荷量为q，不计粒子重力和相互作用力。求：

（1）若带正电粒子垂直打在N板上，I区磁场的磁感应强度；

（2）在第（1）问中，调节电场强度的大小，N板上的亮斑刚好消失时的场强E；

（3）若区域II的电场强度，要使M板出现亮斑，I区磁场的最小磁感应强度。

Answer 1

【答案】（1）（2）（3）

【解析】

【试题分析】(1)若质子垂直打在N板上，质子出磁场时必须与磁场的右边界垂直，画出质子在磁场中的运动轨迹，由几何关系求出轨迹半径，由牛顿第二定律求磁感应强度B1；(2)要使N板上的亮斑恰好消失，质子进入电场后须做匀减速直线运动，到达N板的速度恰好为零．由动能定理求场强E；(3)设质子从磁场进入电场时速度方向与虚线边界间的夹角为θ，进入电场后做类斜上抛运动，当质子刚要达到N板时，沿电场线方向速度减小为零，如图所示，此时质子恰好能返回磁场打在M板上产生亮班，而此时的磁感应强度最小．研究电场中沿电场线方向的运动，由动能定理求出θ．根据几何关系求出磁场中轨迹半径，即可求解I区磁场的最小磁感应强度B2．

(1) 带正电粒子在磁场中洛伦兹力提供向心力，

解得

若带正电粒子垂直打在N板上，必须粒子出磁场时须与磁场的右边界垂直，如图甲所示，

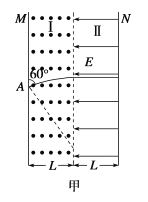
由几何关系得r1cos60°＝L

得：r1＝2L

联立解得Ⅰ区磁场的磁感应强度为

(2)粒子进入电场后逆着电场线做匀减速直线运动，调节电场强度的大小，N板上的亮斑刚好消失时，粒子的速度刚好减为零，由动能定理得

N板上的亮斑刚好消失时的场强为

(3)设粒子从磁场进入电场时速度方向与虚线边界间的夹角为θ，进入电场后做类斜上抛运动，当质子刚要到达N板时，沿电场线方向速度减小为零，如图乙所示，此时粒子恰好能返回磁场打在M板上产生亮斑，而此时的磁场的磁感应强度最小．

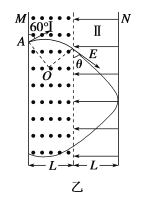
沿电场方向，由动能定理得

得θ＝30°

在磁场中，由几何关系知r2sin 60°＋r2sin 30°＝L

得

故Ⅰ区磁场的最小磁感应强度为