题目内容
3. 一根轻绳,两端分别固定在竖直棒上相距为L的A、B两点,一个质量为m的光滑小圆环套在绳子上,当竖直棒以一定的角速度转动时,圆环以A为圆心在水平面上做匀速圆周运动,这时轻绳上端与竖直棒成45°夹角,如图所示,求竖直棒转动的角速度.(重力加速度为g)
一根轻绳,两端分别固定在竖直棒上相距为L的A、B两点,一个质量为m的光滑小圆环套在绳子上,当竖直棒以一定的角速度转动时,圆环以A为圆心在水平面上做匀速圆周运动,这时轻绳上端与竖直棒成45°夹角,如图所示,求竖直棒转动的角速度.(重力加速度为g)
分析 小圆环受到重力和两个拉力,竖直方向上合力等于零,水平方向上的合力提供圆周运动的向心力,根据牛顿第二定律求出竖直棒转动的角速度.
解答 解:对小圆环受力分析如图所示:
小圆环在竖直方向上受力平衡:
Tcos45°=mg…①
小圆环在水平方向上做匀速圆周运动:
T+Tcos45°=mLω2…②
由①和②得小圆环转动的角速度为:
ω=$\sqrt{\frac{(\sqrt{2}+1)g}{L}}$.
答:竖直棒转动的角速度为$\sqrt{\frac{(\sqrt{2}+1)g}{L}}$.
点评 解决本题的关键搞清圆周运动向心力的来源,结合牛顿第二定律进行求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.一物体自t=0时开始做直线运动,其速度图线如图所示.下列选项正确的是( )


| A. | 在0~6s内,物体离出发点的最远距离为30m | |
| B. | 在0~6s内,物体经过的路程为40m | |
| C. | 在0~4s内,物体的平均速率为5m/s | |
| D. | 在5~6s 内,物体所受的合外力做负功 |
18.关于匀速圆周运动,下面说法正确的是( )
| A. | 物体做匀速圆周运动的过程中所受力的合力大小一定是不变的 | |
| B. | 物体做匀速圆周运动的过程中所受的各个力的大小和方向必定是不变的 | |
| C. | 匀速圆周运动属于加速度不变的运动 | |
| D. | 匀速圆周运动属于匀速运动 |
8.下述关于用多用表欧姆档测电阻的说法中正确的是( )
| A. | 测量电阻时如果指针偏转过大,应将选择开关S拨至倍率较小的档位 | |
| B. | 测量定值电阻时,如果红、黑表笔分别插在负、正插孔,不会影响测量结果 | |
| C. | 测量电路中的某个电阻,应该把该电阻与电路断开 | |
| D. | 测量阻值不同的电阻时都必须重新调零 |
15. 酒精测试仪用于机动车驾驶人员是否酗酒及其他严禁酒后作业人员的现场检测.它是一种二氧化锡半导体型酒精气体传感器,酒精气体传感器的电阻随酒精气体浓度的变化而变化,在如图所示的电路中,不同的酒精气体浓度对应着传感器的不同电阻,这样,电压表的指针就与酒精气体浓度有了对应关系.如果二氧化锡半导体型酒精气体传感器电阻的倒数与酒精气体的浓度成正比,那么,电压表示数U与酒精气体浓度c之间的对应关系正确的是( )
酒精测试仪用于机动车驾驶人员是否酗酒及其他严禁酒后作业人员的现场检测.它是一种二氧化锡半导体型酒精气体传感器,酒精气体传感器的电阻随酒精气体浓度的变化而变化,在如图所示的电路中,不同的酒精气体浓度对应着传感器的不同电阻,这样,电压表的指针就与酒精气体浓度有了对应关系.如果二氧化锡半导体型酒精气体传感器电阻的倒数与酒精气体的浓度成正比,那么,电压表示数U与酒精气体浓度c之间的对应关系正确的是( )
 酒精测试仪用于机动车驾驶人员是否酗酒及其他严禁酒后作业人员的现场检测.它是一种二氧化锡半导体型酒精气体传感器,酒精气体传感器的电阻随酒精气体浓度的变化而变化,在如图所示的电路中,不同的酒精气体浓度对应着传感器的不同电阻,这样,电压表的指针就与酒精气体浓度有了对应关系.如果二氧化锡半导体型酒精气体传感器电阻的倒数与酒精气体的浓度成正比,那么,电压表示数U与酒精气体浓度c之间的对应关系正确的是( )
酒精测试仪用于机动车驾驶人员是否酗酒及其他严禁酒后作业人员的现场检测.它是一种二氧化锡半导体型酒精气体传感器,酒精气体传感器的电阻随酒精气体浓度的变化而变化,在如图所示的电路中,不同的酒精气体浓度对应着传感器的不同电阻,这样,电压表的指针就与酒精气体浓度有了对应关系.如果二氧化锡半导体型酒精气体传感器电阻的倒数与酒精气体的浓度成正比,那么,电压表示数U与酒精气体浓度c之间的对应关系正确的是( )| A. | U越大,表示c越大,c与U成正比 | |
| B. | U越大,表示c越大,但是c与U不成正比 | |
| C. | U越大,表示c越小,c与U成反比 | |
| D. | U越大,表示c越小,但是c与U不成反比 |
12.下图中描述质点做匀速直线运动的是( )
| A. |  | B. |  | C. |  | D. |  |
8.如图所示是某质点做直线运动的v-t图象,由图可知这个质点的运动情况是( )
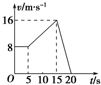

| A. | 前15s做的是匀变速运动 | |
| B. | 10s时的加速度比18s时的加速度大 | |
| C. | 质点15s末离出发点最远,20秒末回到出发点 | |
| D. | 质点20s末离出发点最远 |
 如图所示为某高楼电梯上升的速度图象,试求:
如图所示为某高楼电梯上升的速度图象,试求: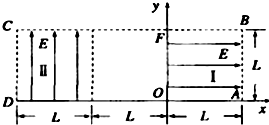 如图所示为研究电子枪中电子在电场中运动的简化模型示意图.在Oxy平面的ABCD区域内,存在两个场强大小均为E的匀强电场Ⅰ和Ⅱ,两电场的边界均是边长为L的正方形(不计电子所受重力).
如图所示为研究电子枪中电子在电场中运动的简化模型示意图.在Oxy平面的ABCD区域内,存在两个场强大小均为E的匀强电场Ⅰ和Ⅱ,两电场的边界均是边长为L的正方形(不计电子所受重力).