题目内容
图中所示x,y,z为三个物块，K为轻质弹簧，L为轻线. 系统处于平衡状态，现若将L突然剪断，用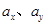
分别表示刚剪断时x、y的加速度，则有（ ）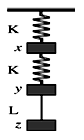
A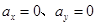． | B． |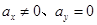
C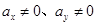． | D． |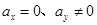
D
解析试题分析：将L突然剪断后，线的拉力立即就没有了，所以y原来受到的线的拉力没有了，而上面受到的弹簧的拉力不变，所以y就有了合力，产生了加速度，所以ay≠0，对于物体x，由于上下的弹簧的拉力都没发生变化，x的受力不变，加速度为0，故D选项正确．
考点： 牛顿第二定律
阅读快车系列答案
如图所示，一粗糙的水平传送带以恒定的速度v1沿顺时针方向运动，传送带的左、右两端皆有一与传送带等高的光滑水平面，一物体以恒定的速度v2沿水平面分别从左、右两端滑上传送带，下列说法正确的是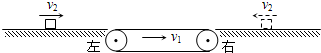
| A．物体从右端滑到左端所须的时间一定大于物体从左端滑到右端的时间 |
| B．若v2<v1，物体从左端滑上传送带必然先做加速运动，再做匀速运动 |
| C．若v2<v1，物体从右端滑上传送带，则物体可能到达左端 |
| D．若v2<v1，物体从右端滑上传送带又回到右端，在此过程中物体先做减速运动，再做加速运动 |
在电梯内的地板上，竖直放置一根轻质弹簧，弹簧上端固定一个质量为m的物体。当电梯匀速运动时，弹簧被压缩了x，某时刻后观察到弹簧又被继续压缩了x/10。则电梯在此时刻后的运动情况可能是
| A．以大小为11g/10的加速度加速上升 |
| B．以大小为11g/10的加速度减速上升 |
| C．以大小为g/10的加速度加速下降 |
| D．以大小为g/10的加速度减速下降 |
如图所示，在光滑平面上有一静止小车，小车上静止地放置着一小物块，物块和小车间的动摩擦因数为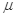
＝0.3，用水平恒力F拉动小车，下列关于物块的加速度
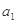和小车的加速度
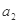。当水平恒力F取不同值时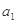，与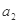的值可能为（当地重力加速度g取
）
A． ， |
B． ， |
C． ， |
D．， |
如图所示，轻质不可伸长的细绳，绕过光滑定滑轮C，与质量为m的物体A连接，A放在倾角为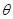
的光滑斜面上，绳的另一端和套在固定竖直杆上的物体B连接。现BC连线恰沿水平方向，从当前位置开始B以速度v0匀速下滑。设绳子的张力为T，在此后的运动过程中，下列说法正确的是 （ ）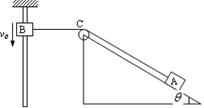
| A．物体A做加速运动 |
| B．物体A做匀速运动 |
C．T可能小于 |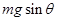
| D．T一定大于 |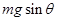
如图，两个质量分别为m1="3" kg、m2 = 2kg的物体置于光滑的水平面上，中间用轻质弹簧秤连接。两个大小分别为F1 =" 30" N、F2 =" 20" N的水平拉力分别作用在m1、m2上，则（ ）
| A．弹簧秤的示数是50N |
| B．弹簧秤的示数是24 N |
| C．在突然撤去F2的瞬间，m1的加速度大小为2 m/s2 |
| D．在突然撤去F2的瞬间，m2的加速度大小为12 m/s2 |
如图所示，有一个正方形的匀强磁场区域abcd，e是ad的中点，f是cd的中点，如果在a点沿对角线方向以速度v射入一带负电的带电粒子(带电粒子重力不计)，恰好从e点射出，则( )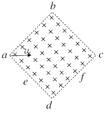
| A．如果粒子的速度增大为原来的二倍，将从d点射出 |
| B．如果粒子的速度增大为原来的三倍，将从f点射出 |
| C．如果粒子的速度不变，磁场的磁感应强度变为原来的二倍，也将从d点射出 |
| D．只改变粒子的速度使其分别从e、d、f点射出时，从e点射出所用时间最短 |
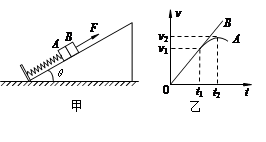
如图(a)所示，用一水平外力F拉着一个静止在倾角为θ的光滑斜面上的物体，逐渐增大F，物体做变加速运动，其加速度a随外力F变化的图像如图(b)所示，若重力加速度g取10m/s2。根据图(b)中所提供的信息可以计算出
| A．加速度从2m/s2增加到6m/s2的过程中物体的速度变化量 |
| B．斜面的倾角 |
| C．物体的质量 |
| D．加速度为6m/s2时物体的速度 |