��Ŀ����
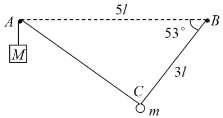
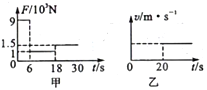
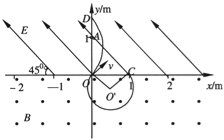
����Ŀ������ͼ��ʾ��ֱ�������У�x����Ϸ�������x���������45���б�����·�����ǿ�糡����ǿ�Ĵ�СΪE��![]() ��104V/m��x����·��д�ֱ��xOy���������ǿ�ų����Ÿ�Ӧǿ�ȵĴ�СΪB��2��10-2T����һ���Ⱥ�Ϊ
��104V/m��x����·��д�ֱ��xOy���������ǿ�ų����Ÿ�Ӧǿ�ȵĴ�СΪB��2��10-2T����һ���Ⱥ�Ϊ![]() =2��108C/kg�������ɴ�����Ϊ��0��1����A�㴦�ɾ�ֹ�ͷţ�������ܵ��������Բ��ƣ���1����ɴ��ͷŵ���һ�ν���ų�ʱ���õ�ʱ�䣻
=2��108C/kg�������ɴ�����Ϊ��0��1����A�㴦�ɾ�ֹ�ͷţ�������ܵ��������Բ��ƣ���1����ɴ��ͷŵ���һ�ν���ų�ʱ���õ�ʱ�䣻
��2������ڴų�����Բ���˶��İ뾶��������λ��Ч���֣���
��3������ɵڶ��ε���x����ʱ���糡����������ǿ��С���䣬��ȷ����ɵ���y��ʱ��λ�����꣮
���𰸡���1��10-6s����2��0.71m����3����0��8����
���������⣺��1����ͼ����ɴ�A���ȼ����˶��˶���x���C��Ĺ��̣�
�S=AC=![]() m
m
���ٶ�a=![]() =2
=2![]() ��1012m/s2
��1012m/s2
ʱ��t=![]() =10��6s
=10��6s
��2����ɵ���C����ٶ�Ϊ
v=at=2![]() ��106m/s
��106m/s
�ٶȷ�����x���������45���ǣ��ڴų���
�˶�ʱ
��qvB=![]()
��R=![]() =
=![]() m
m
������ڴų��е�ƫת�뾶Ϊ0.71m
��3���켣Բ��x���ཻ���ҳ�Ϊ��x=![]() R=1m�����Ե�ɴ�����ԭ��O�ٴν���糡�У����ٶȷ�����糡����ֱ������ڵ糡������ƽ���˶���
R=1m�����Ե�ɴ�����ԭ��O�ٴν���糡�У����ٶȷ�����糡����ֱ������ڵ糡������ƽ���˶���
�赽��y���ʱ��Ϊt������
tan45��=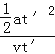
���t��=2��10��6s
����ƽ���˶��д�ֱ�ڵ糡�����λ��L=vt��=4![]() m
m
y=![]() =8m
=8m
����ɵ���y���ϵĵ������Ϊ��0��8��
�𣺣�1����ɴ��ͷŵ���һ�ν���ų�ʱ���õ�ʱ��10��6s��
��2������ڴų�����Բ���˶��İ뾶0.71m��
��3������ɵڶ��ε���x����ʱ���糡����������ǿ��С���䣬��ȷ����ɵ���y��ʱ��λ�����꣨0��8����

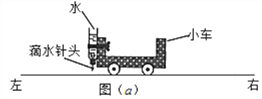
����Ŀ����1����ͼ��ʾ�����������һ�����������һ֧��ɫ���ʡ����ͬ��ǣ��һ����Լ1 cm�ij�ֽ����ʹֽ������ı�������ֱ����ǰ�ƶ���ÿ��1s���û�����ֽ���ϵ�һ���㡣�㻹������ϰ��1s�ھ��ȵص��������㡣��������������һ̨��������ʱ��������ʵ���ֽ֪���ٶ�Խ����������ľ���Խ___________��ֽ�����ٶ���������������ʾ��ʱ��__________��������������û������Ӱ�졣

��2��С����ͬһ������ʱ���ڹ̶�Ƶ���£��y��С������ֽ���ס��ҡ����������˶��ٶȣ�ÿ�γ��Ӷ������������˶����Ķ�ֽ���ij��ȶ���ͬ����ͼ��������������ȷ��
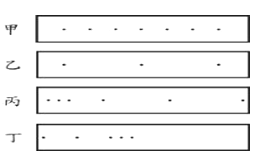
A��ֽ���״����ȣ���ʾ���ӵ��˶������ٵģ����ٶ����㡣 |
B��ֽ������ʾ��ƽ���ٶ���ֽ������ͬ |
C��ֽ������ʾ��С�����˶����ȿ���� |
D��ֽ������ʾ��С�����˶���������� |