题目内容
1.长为l的动车组以加速度a匀加速通过某处的平直隧道,若动车组通过隧道入口的时间为t1,动车组通过隧道出口的时间为t2,求隧道的长度和位于动车中点处的乘客通过隧道的时间.分析 动车做匀加速直线运动,对过隧道人口过程、通过隧道出口过程、动车车头通过隧道过程分别根据运动学公式列式,然后联立求解即可.
解答 解:取动车车头为研究对象,设动车车头到达入口处速度为v0,到达出口处速度为vt,由匀变速直线运动规律,有:
入口处:L=v0t1$+\frac{1}{2}$at${\;}_{1}^{2}$
出口处:L=vtt2$+\frac{1}{2}$at${\;}_{2}^{2}$
隧道的长度为:x=$\frac{{v}_{t}^{2}-{v}_{0}^{2}}{2a}$=$\frac{(\frac{L}{{t}_{1}}-\frac{1}{2}a{t}_{2}^{\;})^{2}-(\frac{L}{{t}_{2}}-\frac{1}{2}a{t}_{2})^{2}}{2a}$
由加速度定义,有:t=$\frac{{v}_{t}-{v}_{0}}{a}$
解得:t=$\frac{L}{a}$($\frac{1}{{t}_{2}}-\frac{1}{{t}_{1}})$+$\frac{{t}_{1}-{t}_{2}}{2}$
位于动车中点处的乘客通过隧道的时间与动车车头通过隧道的时间相同,为:$\frac{L}{a}$($\frac{1}{{t}_{2}}-\frac{1}{{t}_{1}})$+$\frac{{t}_{1}-{t}_{2}}{2}$.
答:隧道的长度为$\frac{(\frac{L}{{t}_{1}}-\frac{1}{2}a{t}_{2}^{\;})^{2}-(\frac{L}{{t}_{2}}-\frac{1}{2}a{t}_{2})^{2}}{2a}$;
位于动车中点处的乘客通过隧道的时间为$\frac{L}{a}$($\frac{1}{{t}_{2}}-\frac{1}{{t}_{1}})$+$\frac{{t}_{1}-{t}_{2}}{2}$.
点评 本题关键是明确动车的运动规律,然后选择过程列式后联立求解,一定要会解方程组.

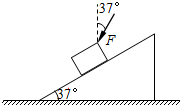 如图所示,一倾角为37°的斜劈放在水平地面上,一物体沿斜劈恰能匀速下滑.现给物体施加一个与竖直方向夹角为37°斜向下的力F=5N作用,斜劈仍静止,sin37°=0.6,cos37°=0.8.则( )
如图所示,一倾角为37°的斜劈放在水平地面上,一物体沿斜劈恰能匀速下滑.现给物体施加一个与竖直方向夹角为37°斜向下的力F=5N作用,斜劈仍静止,sin37°=0.6,cos37°=0.8.则( )| A. | 物体仍能沿斜面匀速下滑 | B. | 地面对斜劈的支持力增大4N | ||
| C. | 地面对斜劈的摩擦力大小为零 | D. | 地面对斜劈的摩擦力大小为3N |
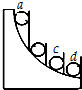
| A. | a球 | B. | b球 | C. | c球 | D. | d球 |
 如图所示,在真空中有两个固定的点电荷A、B,|qA|=|qB|=q,A、B间的距离为r,图中画出了其中一根电场线,a、b、c、d位于正方形的四个顶点,其中a、c在A、B的连线上,b、d在A、B连线的中垂线上,下列说法正确的是( )
如图所示,在真空中有两个固定的点电荷A、B,|qA|=|qB|=q,A、B间的距离为r,图中画出了其中一根电场线,a、b、c、d位于正方形的四个顶点,其中a、c在A、B的连线上,b、d在A、B连线的中垂线上,下列说法正确的是( )| A. | 若B是正电荷,则b点的场强Eb>$\frac{2\sqrt{2}k{q}^{2}}{{r}^{2}}$ | |
| B. | 若a、c两点的场强大小相等,则B一定是正电荷 | |
| C. | 若Ubd=0,则A、B一定是异种电荷 | |
| D. | 若ϕa=ϕc,则B一定是负电荷 |
| A. | 布朗运动就是液体分子的无规则运动 | |
| B. | 空气相对湿度越大时,空气中水蒸气压强越接近饱和汽压,水蒸发越快 | |
| C. | 热量不能自发地从低温物体传给高温物体 | |
| D. | 利用浅层海水和深层海水之间的温度差制造一种热机,将海水的一部分内能转化为机械能是可能的 |
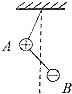
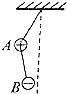
 如图所示,A、B两带电小球的质量分布为2m,m,所带电量分布为3q和-q,两球间用绝缘细线相连,A球又用等长的绝缘细线悬挂在天花板上(两球的大小可忽略不计),在两球所在空间有水平向左的匀强电场,电场强度为E,平衡时细线都被拉紧,平衡时的可能位置是图中的( )
如图所示,A、B两带电小球的质量分布为2m,m,所带电量分布为3q和-q,两球间用绝缘细线相连,A球又用等长的绝缘细线悬挂在天花板上(两球的大小可忽略不计),在两球所在空间有水平向左的匀强电场,电场强度为E,平衡时细线都被拉紧,平衡时的可能位置是图中的( )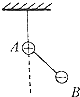

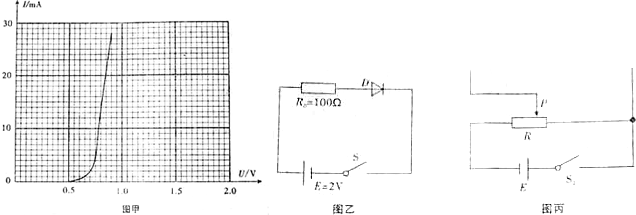
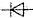 )的正向伏安特性曲线.图丙仅画出了他设计的部分电路图,请你补全完成该实验的电路图,并标明各元件的符号.
)的正向伏安特性曲线.图丙仅画出了他设计的部分电路图,请你补全完成该实验的电路图,并标明各元件的符号.