题目内容
如图所示，弧形轨道的下端与竖直圆轨道相切，使小球(视为质点)从弧形轨道上的P点无初速滑下，小球进入圆轨道底端M点后沿圆轨道运动，已知圆轨道的半径为R，P点到水平面的距离为h，弧形轨道与圆轨道均光滑，则下列说法中正确的有（ ）
| A．h<R时，h越大，小球滑过M点后能达到的最大高度越高 |
| B．R < h<2R时，小球滑过M点后能达到的最大高度为h |
| C．h>2R时，小球一定能经过圆轨道最高点N |
| D．h=R时，小球滑过M点时对圆轨道的压力等于其重力的3倍 |
AD
试题分析：当h<R时，根据机械能守恒小球滑过M点后能达到的最大高度等于h，故A正确；当R < h<2R时，小球滑过M点后能达到的最大高度大于R，而大于R后要不脱离轨道小球的速度需大于零，根据机械能守恒
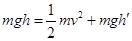，故
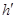小于h，所以B错误；小球要过最高点N，在N点的速度最小为
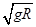，所以h>2R时，小球不一定能经过圆轨道最高点N，故C错误；h=R时，小球滑过M点时的速度
，在M点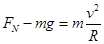
，联立可得：FN=3mg，所以D正确。
练习册系列答案
相关题目
