题目内容
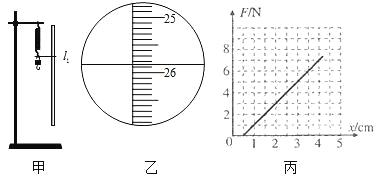
【题目】如图所示,倾角θ=30°的光滑斜面固定在水平地面上,斜面顶端a离地高度h=2.5 cm,整个装置处于水平向左的匀强电场中.一个质量m=0.3 kg,带电量q=+0.01 C的物体(可视为质点)从斜面顶端静止释放,经过t=0.2 s到达斜面底端b点(g取10 m/s2).求:

(1)物体到达斜面底端b时的速度大小;
(2)电场强度E的大小;
(3)电场中a到b两点之间的电势差.
【答案】(1)0.5 m/s.(2)50![]() V/m.(3) -3.75 V.
V/m.(3) -3.75 V.
【解析】(1)斜面的长度为:L=![]() =2h=0.05m,
=2h=0.05m,
下滑的加速度为:![]()
底端速度为:v=at=0.5m/s
(2)由牛顿第二定律得:mgsin30°-qEcos30°=ma
解得:E=50![]() V/m
V/m
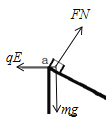
(3)电场中a到b两点之间的电势差:Uab=-ELcos30°=-3.75V

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
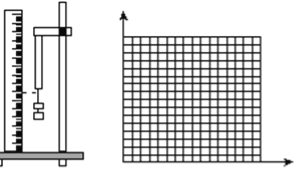
【题目】某同学在“用打点计时器测速度”的实验中,用打点计时器记录了被小车拖动的纸带的运动情况,在纸带上确定出A、B、C、D、E、F、G共7个计数点。其相邻点间的距离如图所示,每两个相邻的测量点之间的时间间隔为0.10s。
(1)试根据纸带上各个计数点间的距离,计算出打下B、C、D、E、F 5个点时小车的瞬时速度,并将各个速度值填入表中。(要求保留三位有效数字)
![]()
vB | vC | vD | vE | vF | |
数值/(m·s-1) | ___ | ___ | ___ | ___ | ___ |
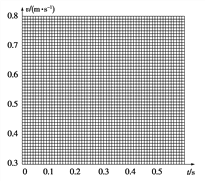
(2)将B、C、D、E、F各个时刻的瞬时速度标在直角坐标系中,并在图中画出小车的瞬时速度随时间变化的关系图线________。