题目内容
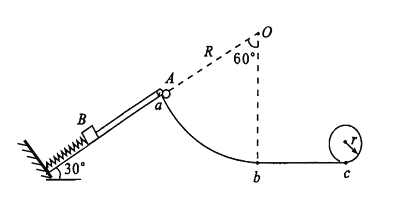
【题目】如图所示，倾角θ=30°的光滑斜面上，一轻质弹簧一端固定在挡板上，另一端连接质量mB=0.5kg的物块B，B通过轻质细绳跨过光滑定滑轮与质量mA=4kg的物块A连接，细绳平行于斜面，A在外力作用下静止在圆心角为α=60°、半径R=lm的光滑圆弧轨道的顶端a处，此时绳子恰好拉直且无张力；圆弧轨道最低端b与粗糙水平轨道bc相切，bc与一个半径r=0.12m的光滑圆轨道平滑连接，静止释放A，当A滑至6时，弹簧的弹力与物块A在顶端d处时相等，此时绳子断裂，已知bc长度为d=0.8m，求：(g取l0m/s2)
(1)轻质弹簧的劲度系数k；
(2)物块A滑至b处，绳子断后瞬间，圆轨道对物块A的支持力大小；
(3)为了让物块A能进入圆轨道且不脱轨，则物体与水平轨道bc间的动摩擦因数μ应满足什么条件？
【答案】（1）
（2）
（3）
或
【解析】（1）A位于a处时，绳无张力弹簧处于压缩状态，设压缩量为
对B由平衡条件可以得到： 
当A滑至b时，弹簧处于拉伸状态，弹力与物块A在顶端a处时相等，则伸长量也为x，由几何关系可知： 
，代入数据解得： 
；
（2）物块A在a处和在b处时，弹簧的形变量相同，弹性势能相同
由机械能守恒有： 
将A在b处，由速度分解关系有： 
代入数据解得： 
在b处，对A由牛顿定律有： 
代入数据解得支持力： 
。
（3）物块A不脱离圆形轨道有两种情况：
①不超过圆轨道上与圆心的等高点
由动能定理，恰能进入圆轨道时需要满足： 
恰能到圆心等高处时需要满足条件： 
代入数据解得： 
， 
②过圆轨道最高点，则恰好过最高点时： 
由动能定理有： 
代入数据解得： 
为使物块A能进入圆轨道且不脱轨，有： 
或
。
练习册系列答案
互动课堂系列答案
激活思维智能训练课时导学练系列答案
相关题目
