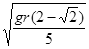题目内容
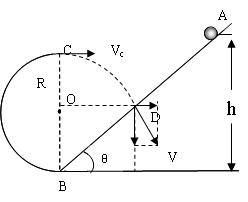
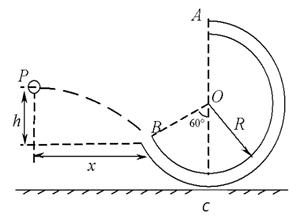
如图,光滑半圆弧轨道BC与光滑斜面AB在B点平滑连接,圆弧半径为R=0.4m,一半径很小,质量为m=0.2kg的小球从光滑斜面上A点由静止释放,恰好能通过圆弧轨道最高点C,(小球在轨道连接处无机械能损失,不计空气阻力,g=10 m/s2)求:

(1)小球最初释放的高度h;
(2)若要使小球离开C点恰好垂直撞击到斜面上,斜面的倾角θ的正切值为多大?

(1)小球最初释放的高度h;
(2)若要使小球离开C点恰好垂直撞击到斜面上,斜面的倾角θ的正切值为多大?
(1)1m (2) tanθ=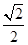
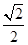
试题分析:(1)由物体恰好通过最高点C,有:mg=m
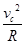 ①(2分)
①(2分)物体从A点运动到C点机械能守恒,所以:mg(h-2R)=
 ②(2分)
②(2分)联立①②代入数据解得h=1m(2分)
(2)设小球落到斜面上的点为D,如图所示,设DB=a,根据平抛运动的规律和几何知识得:
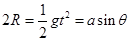 ③(1分)
③(1分)水平方向有:
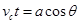 ④(1分)
④(1分)tanθ=
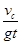 ⑤(2分)
⑤(2分)联立①③④⑤解得:tanθ=
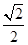 (2分)
(2分)
练习册系列答案
相关题目

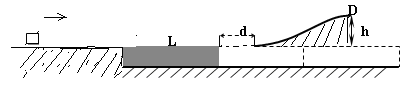

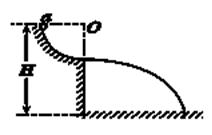

 B. 小于
B. 小于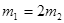 ,让质量为m1的小球静止释放,当其到达碗底时质量为m2的小球速度为多大( )
,让质量为m1的小球静止释放,当其到达碗底时质量为m2的小球速度为多大( )