题目内容
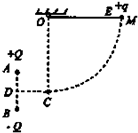 如图所示,固定在同一竖直线上的A、B是两个带等量异种电荷(电荷量为Q=2×10-6C)的点电荷,其中A带正电.D、C在它们连线的垂直平分线上,且A、B、C三点构成一个边长为d=10cm的等边三角形.另有一个带电小球E,质量为m=0.02kg,电荷量为q=+1×10-7C(可视为点电荷),被长为L=40cm的绝缘轻质细线悬挂于O点,O点在C点的正上方.现把小球E拉起到M点,使细线水平绷直且与A、B、C处于同一竖直平面内.小球E由静止开始释放,向下运动到最低点C时,速度为v=4m/s.已知静电力常量为k=9×109N?m2/C2,且取D点电势为零.试求:
如图所示,固定在同一竖直线上的A、B是两个带等量异种电荷(电荷量为Q=2×10-6C)的点电荷,其中A带正电.D、C在它们连线的垂直平分线上,且A、B、C三点构成一个边长为d=10cm的等边三角形.另有一个带电小球E,质量为m=0.02kg,电荷量为q=+1×10-7C(可视为点电荷),被长为L=40cm的绝缘轻质细线悬挂于O点,O点在C点的正上方.现把小球E拉起到M点,使细线水平绷直且与A、B、C处于同一竖直平面内.小球E由静止开始释放,向下运动到最低点C时,速度为v=4m/s.已知静电力常量为k=9×109N?m2/C2,且取D点电势为零.试求:(1)在A、B所形成的电场中M点的电势?M?
(2)绝缘细线在C点所受的拉力T?
分析:(1)D点的电势为零,求M点的电势,只需求出UMD,由UMD=φM-φD即可求出φM.电势差对应一个过程中电场力做的功,所以第一步先求由M到D过程中电场力做的功,再由UMD=
求得.
(2)小球E向下运动到最低点C时,速度为v,运动为圆周运动.可受力分析后找出向心力,由向心力公式进行求解.
| WMD |
| q |
(2)小球E向下运动到最低点C时,速度为v,运动为圆周运动.可受力分析后找出向心力,由向心力公式进行求解.
解答:解:(1)小球从M点到C点:
设:M点与C点之间的电势差为U:
根据动能定理列式得:设电场力做功w1,重力做功w2
W1+W2=
mv2-0; 即:qU+mgL=
mv2;
则U=
又U=φm-φc,φc=φd=0 (c,d两点在同一等势线上)
所以φM=
=
V=8×105V.
(2)分析C点受力情况如图:
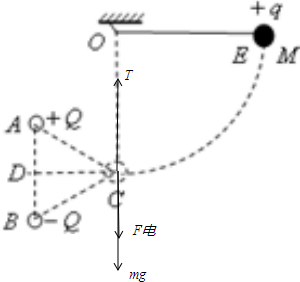
C点受到A,B两点的电场力的合力方向竖直向下
大小为:
又圆周运动可知:
T-mg-
=
所以:T=mg+
+
=0.02×10+
+
=1.18N;
答:(1)在A、B所形成的电场中,M点的电势8×105V;
(2)绝缘细线在C点所受到的拉力1.18N.
设:M点与C点之间的电势差为U:
根据动能定理列式得:设电场力做功w1,重力做功w2
W1+W2=
| 1 |
| 2 |
| 1 |
| 2 |
则U=
| ||
| q |
又U=φm-φc,φc=φd=0 (c,d两点在同一等势线上)
所以φM=
| ||
| q |
| ||
| 1×10-7 |
(2)分析C点受力情况如图:

C点受到A,B两点的电场力的合力方向竖直向下
大小为:
| kQq |
| d2 |
T-mg-
| kQq |
| d2 |
| mv2 |
| L |
所以:T=mg+
| kQq |
| d2 |
| mv2 |
| L |
| 9×109×2×10-6×10-7 |
| 0.12 |
| 0.02×42 |
| 0.4 |
答:(1)在A、B所形成的电场中,M点的电势8×105V;
(2)绝缘细线在C点所受到的拉力1.18N.
点评:电场力与电势差之间的关系要牢固的掌握,对于圆周运动,只需要找出向心力,列方程即可.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图所示,固定在同一水平面内的两根平行长直金属导轨的间距为L,其右端接有阻值为R的电阻,整个装置处在竖直向上磁感应强度大小为B的匀强磁场中.一根质量为m(质量分布均匀)的导体杆ab垂直于导轨放置,且与两导轨保持良好接触,杆与导轨之间的动摩擦因数为μ.现杆在水平向左、垂直于杆的恒力F作用下从静止开始沿导轨运动距离d时,速度恰好达到最大(运动过程中杆始终与导轨保持垂直).设杆接入电路的电阻为r,导轨电阻不计,重力加速度大小为g.则此过程( )
如图所示,固定在同一水平面内的两根平行长直金属导轨的间距为L,其右端接有阻值为R的电阻,整个装置处在竖直向上磁感应强度大小为B的匀强磁场中.一根质量为m(质量分布均匀)的导体杆ab垂直于导轨放置,且与两导轨保持良好接触,杆与导轨之间的动摩擦因数为μ.现杆在水平向左、垂直于杆的恒力F作用下从静止开始沿导轨运动距离d时,速度恰好达到最大(运动过程中杆始终与导轨保持垂直).设杆接入电路的电阻为r,导轨电阻不计,重力加速度大小为g.则此过程( )A、杆的速度最大值为
| ||
B、流过电阻R的电量为
| ||
| C、恒力F做的功与摩擦力做的功之和等于杆动能的变化量 | ||
| D、恒力F做的功与安培力做的功之和大于杆动能的变化量 |
 如图所示,固定在同一水平面内的两根平行长直金属导轨的间距为d,其右端接有阻值为R的电阻,整个装置处在竖直向上、磁感应强度大小为B的匀强磁场中.一质量为m的导体杆ab垂直于导轨放置,且与两导轨保持良好接触,杆与导轨之间的动摩擦因数为μ.现导体杆在水平向左、垂直于杆的恒力F(大小未知)作用下从静止开始运动,沿导轨运动距离L时,恰好达到最大速度vm.运动过程中导体杆始终与导轨保持垂直.设导体杆接入电路的电阻为r,导轨电阻不计,重力加速度为g.求:
如图所示,固定在同一水平面内的两根平行长直金属导轨的间距为d,其右端接有阻值为R的电阻,整个装置处在竖直向上、磁感应强度大小为B的匀强磁场中.一质量为m的导体杆ab垂直于导轨放置,且与两导轨保持良好接触,杆与导轨之间的动摩擦因数为μ.现导体杆在水平向左、垂直于杆的恒力F(大小未知)作用下从静止开始运动,沿导轨运动距离L时,恰好达到最大速度vm.运动过程中导体杆始终与导轨保持垂直.设导体杆接入电路的电阻为r,导轨电阻不计,重力加速度为g.求: 如图所示,固定在同一水平面内的两根平行长直金属导轨的间距为d,其右端接有阻值为R的电阻,整个装置处在竖直向上磁感应强度大小为B的匀强磁场中.一质量为m的导体ab垂直于导轨放置,且与两导轨保持良好接触,导体与导轨之间的动摩擦因数为μ.现导体在水平向左、垂直于导体的恒力F作用下从静止开始沿导轨运动距离L时,速度恰好达到最大(运动过程中始终与导轨保持垂直).设导体接入电路的电阻为r,导轨电阻不计,重力加速度大小为g.则此过程
如图所示,固定在同一水平面内的两根平行长直金属导轨的间距为d,其右端接有阻值为R的电阻,整个装置处在竖直向上磁感应强度大小为B的匀强磁场中.一质量为m的导体ab垂直于导轨放置,且与两导轨保持良好接触,导体与导轨之间的动摩擦因数为μ.现导体在水平向左、垂直于导体的恒力F作用下从静止开始沿导轨运动距离L时,速度恰好达到最大(运动过程中始终与导轨保持垂直).设导体接入电路的电阻为r,导轨电阻不计,重力加速度大小为g.则此过程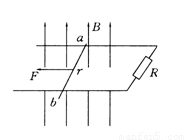

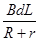 ks5*u
ks5*u