题目内容
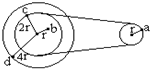 图中所示为一皮带传动装置,右轮的半径为r,a是它边缘上的一点.左侧是一轮轴,大轮的半径为4r,小轮的半径为2r,b点在小轮上,到小轮中心的距离为r.c点和d点分别位于小轮和大轮的边缘上.若在传动过程中,皮带不打滑.则:a,c,d三点的线速度之比Va:Vc:Vd=
图中所示为一皮带传动装置,右轮的半径为r,a是它边缘上的一点.左侧是一轮轴,大轮的半径为4r,小轮的半径为2r,b点在小轮上,到小轮中心的距离为r.c点和d点分别位于小轮和大轮的边缘上.若在传动过程中,皮带不打滑.则:a,c,d三点的线速度之比Va:Vc:Vd=1:1:2
1:1:2
,角速度之比ωa:ωc:ωd=2:1:1
2:1:1
.分析:皮带传动装置,在传动过程中不打滑,则有:共轴的角速度是相同的;同一皮带的与皮带接触边缘的线速度大小是相等的.所以当角速度一定时,线速度与半径成正比;当线速度大小一定时,角速度与半径成反比.因此根据题目条件可知三点的线速度及角速度关系.
解答:解:如图所示,a与c同一皮带下传动,则Va=Vc,因为ra:rc=1:2,所以ωa:ωc=2:1;
c、b、d三点共轴,则ωc=ωb=ωd,因为rb:rc:rd=1:2:4,所以vb:vc:vd=1:2:4;
因此线速度之比Va:Vc:Vd=1:1:2,
角速度之比ωa:ωc:ωd=2:1:1
故答案为:1:1:2;2:1:1
c、b、d三点共轴,则ωc=ωb=ωd,因为rb:rc:rd=1:2:4,所以vb:vc:vd=1:2:4;
因此线速度之比Va:Vc:Vd=1:1:2,
角速度之比ωa:ωc:ωd=2:1:1
故答案为:1:1:2;2:1:1
点评:本题要紧扣隐含条件:共轴的角速度是相同的;同一皮带的与皮带接触边缘的线速度大小是相等的.以此作为突破口;同时能掌握线速度、角速度与半径之间的关系.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
图中所示为一皮带传动装置,右轮的半径为r,a是它边缘上的一点。左侧是一轮轴,大轮的半径为4r,小轮的半径为2r。b点在小轮上,到小轮中心的距离为r。c点和d点分别位于小轮和大轮的边缘上。若在传动过程中,皮带不打滑。则 ( ) 
| A.a点与b点的线速度大小相等 |
| B.a点与b点的角速度大小相等 |
| C.a点与c点的线速度大小相等 |
| D.a点与d点的向心加速度大小相等 |
 图中所示为一皮带传动装置,右轮的半径为r,a是它边缘上的一点.左侧是一轮轴,大轮的半径为4r,小轮的半径为2r.b点在小轮上,到小轮中心的距离为r.c点和d点分别位于小轮和大轮的边缘上.若在传动过程中,皮带不打滑.则( )
图中所示为一皮带传动装置,右轮的半径为r,a是它边缘上的一点.左侧是一轮轴,大轮的半径为4r,小轮的半径为2r.b点在小轮上,到小轮中心的距离为r.c点和d点分别位于小轮和大轮的边缘上.若在传动过程中,皮带不打滑.则( ) 图中所示为一皮带传动装置,右轮的半径为r,a是它边缘上的一点.左侧是一轮轴,大轮的半径为4r,小轮的半径为2r.b点在小轮上,到小轮中心的距离为r.c点和d点分别位于小轮和大轮的边缘上.若在传动过程中,皮带不打滑.则a点、b点、c点的线速度大小之比为
图中所示为一皮带传动装置,右轮的半径为r,a是它边缘上的一点.左侧是一轮轴,大轮的半径为4r,小轮的半径为2r.b点在小轮上,到小轮中心的距离为r.c点和d点分别位于小轮和大轮的边缘上.若在传动过程中,皮带不打滑.则a点、b点、c点的线速度大小之比为