Question

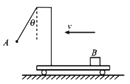
【题目】如图所示，固定在竖直平面内倾角为θ=37°，轨道高度AD=2.4m的倾斜直轨道AB，与水平直轨道BC顺滑连接（在B处有一小段光滑圆弧，小物块经过B点前后的速度大小不变），C点处有墙壁。某一小物块（视为质点）从A点开始静止下滑，到达B点的速度大小为4m/s。假定小物块与AB、BC面的动摩擦因数相等，（sin 37°=0.6，cos 37°=0.8）。则：

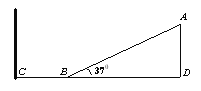
（1）求小物块与AB轨道的动摩擦因数；

（2）为防止小物块在C点撞墙，求BC间距离的最小值。

（3）满足（2）BC的长度，在墙的C点装一弹射装置（长度不计）给物块一初速度v0，要使小物块能返回到A点，求v0至少为多大。

Answer 1

【答案】（1）μ＝0.5（2）1.6m（3）

【解析】

（1）物块在AB面上的加速度大小为a1

由xAB＝＝4m

得a1＝＝2m/s2

由牛顿第二定律得

ma1＝mgsinθ－μmgcosθ

得μ＝0.5

（2）物块在BC面上的加速度大小a2＝μg＝5m/s2

刚好不撞上C点，设BC的长度为xBC.

得xBC＝＝1.6m

BC的长度至少为1.6m

（3）要使滑块能到A点，则到达A点速度最小值为0，物块在AB轨道上滑的加速度为a3，

由牛顿第二定律可得：mgsinθ+μmgcosθ=ma3

得a3=10m/s2，方向沿斜面向下。

由 得

由 得

则v0至少为